The alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by
I=I0sinωt
I=I0sin(ωt+π2)
I=I0sin(ωt−π2)
I=I0sin(ωt−π)
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the alternating emf applied across a capacitor and the resulting current through the circuit.
1. Understand the given emf: The alternating emf is given by the equation:
e=e0sin(ωt)
where e0 is the maximum emf, ω is the angular frequency, and t is time.
2. Know the relationship between current and voltage in a capacitor: In a capacitor, the current i leads the voltage v across it by a phase angle of π2 radians (or 90 degrees). This means that the current reaches its maximum value a quarter cycle before the voltage does.
3. Express the voltage across the capacitor: The voltage across the capacitor can be expressed in terms of the emf:
v=e=e0sin(ωt)
4. Determine the current through the capacitor: Since the current leads the voltage by π2, we can express the current as:
i=I0sin(ωt+π2)
where I0 is the maximum current.
5. Use the trigonometric identity: We know that:
sin(x+π2)=cos(x)
Therefore, we can rewrite the current as:
i=I0cos(ωt)
6. Relate the maximum current to the maximum voltage: The maximum current I0 can be related to the maximum voltage e0 and the capacitance C using the formula:
I0=Cdedt
The derivative of the voltage e with respect to time t is:
dedt=e0ωcos(ωt)
Therefore, the maximum current becomes:
I0=Ce0ω
7. Final expression for the current: Substituting I0 back into the expression for current, we get:
i=Ce0ωcos(ωt)
Conclusion:
The current through the circuit when an alternating emf e=e0sin(ωt) is applied across a capacitor C is given by:
i=Ce0ωcos(ωt)
e=e0sin(ωt)
where e0 is the maximum emf, ω is the angular frequency, and t is time.
v=e=e0sin(ωt)
i=I0sin(ωt+π2)
where I0 is the maximum current.
sin(x+π2)=cos(x)
Therefore, we can rewrite the current as:
i=I0cos(ωt)
I0=Cdedt
The derivative of the voltage e with respect to time t is:
dedt=e0ωcos(ωt)
Therefore, the maximum current becomes:
I0=Ce0ω
i=Ce0ωcos(ωt)
The current through the circuit when an alternating emf e=e0sin(ωt) is applied across a capacitor C is given by:
i=Ce0ωcos(ωt)
Topper's Solved these Questions
Similar Questions
Explain the term 'capacitive reactance'.Show graphically the variation of capacitive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied a across a pure capacitor C.Show mathematically that the current flowing through it leads the applied voltage by a phase angle of π/2
View SolutionAn a.c. emf of e=220 sin ω t is applied across the capacitor, the power consumption is
View Solution
Knowledge Check
An alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
AE0ωLsin(ωt+π/2)BE0ωLsin(ωt−π/2)CE0ωLsin(ωt−π/2)DE0ωLsin(ωt+π/2)If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)
The alternating emf of e=e0 sin ωt is applied across LR series circuit. The impedance and phase angle between current and voltage is
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionAn alternating emf, e=300 sin100πt volt, is applied to a pure resistance of 100 Ω. The rms current through the circuit is
View SolutionThe current through the capacitor in the given circuit is
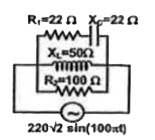
View Solution
