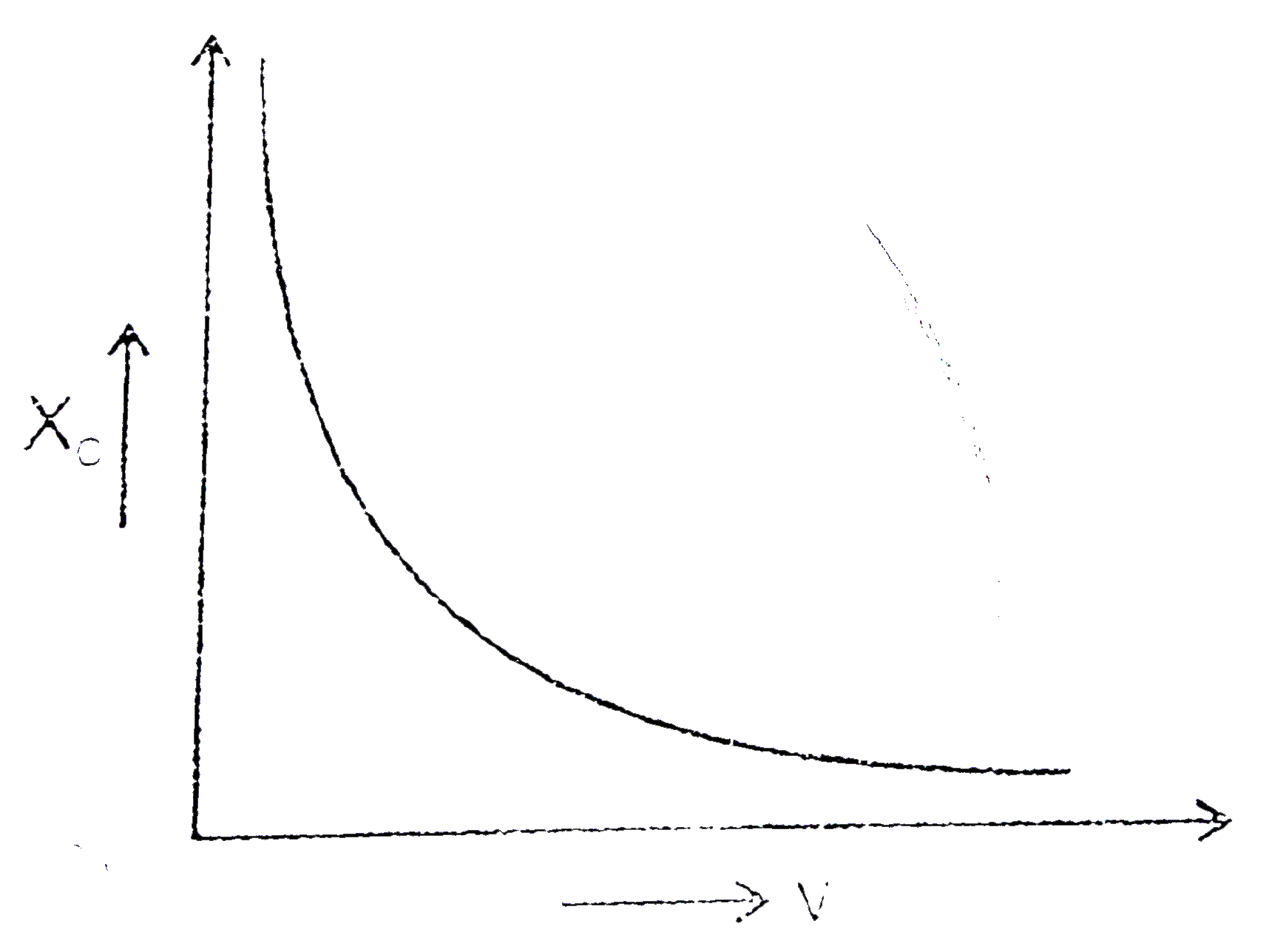
Explain the term 'capacitive reactance'.Show graphically the variation of capacitive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied a across a pure capacitor C.Show mathematically that the current flowing through it leads the applied voltage by a phase angle of π/2
Capacitve reactance:The effective resistance offered by the capacitor C.It is denote by XC its is ohm. The graph between frequency (v) and XC is shown in Fig.
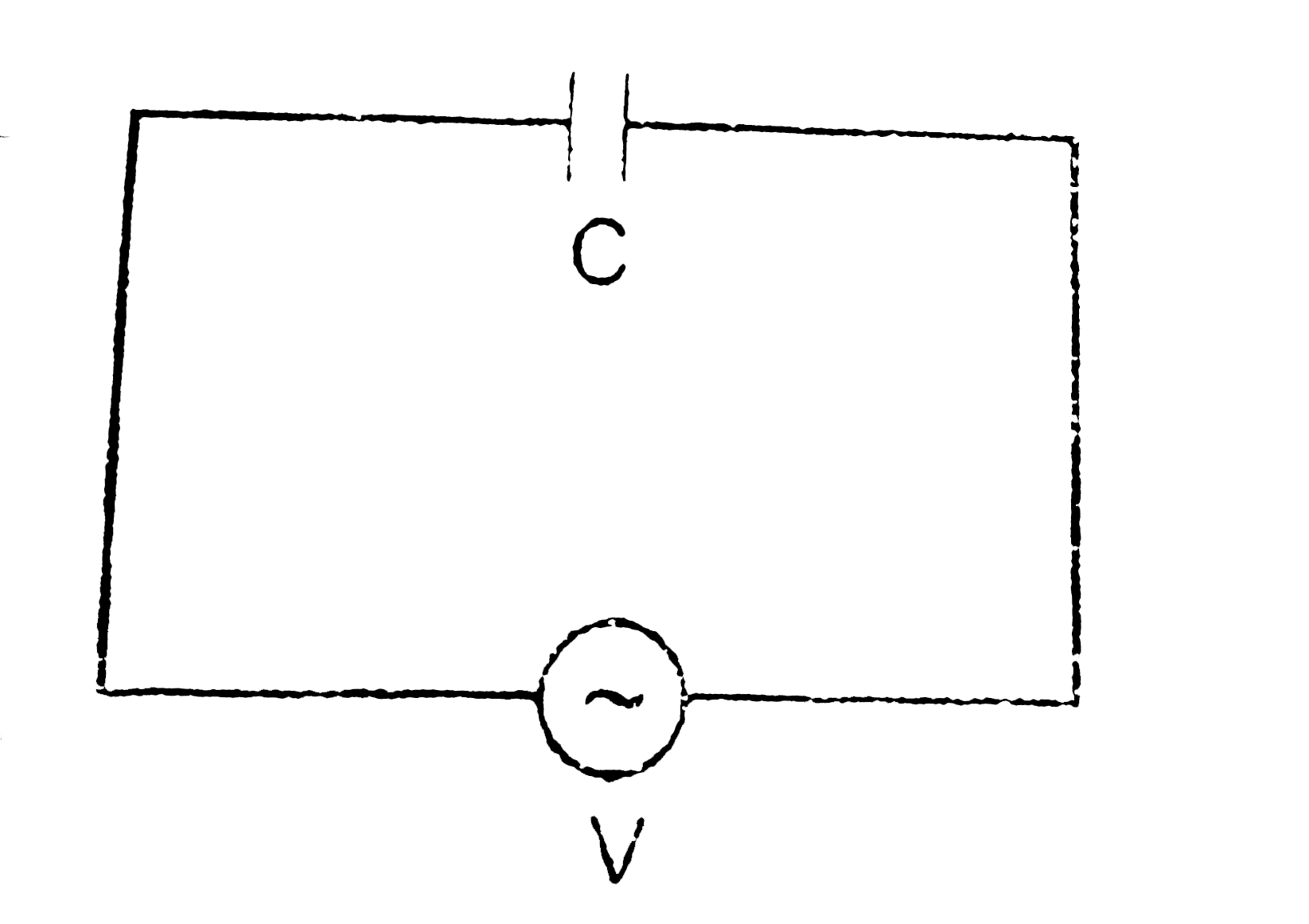
A.C. Source Containing a capacitor:Let a source of alternating e.m.fV=Vmsinwt be connected a capacitor of capacitance C only.
V=Vmsinwt...(i)
At every instant the potential V is given by V=qC⇒Vmsinωt=qC
q=CVmsinωt
If it is instanteious value of current in the circuit at instant t, then
i=dgdt=ddt(CVmsinωt)
i=CVm(cosωt)ω=Vm1/ωCsin(ωt+π2)
The current will be maximum. When (sinωt+π2)
∴im=Vm1/ωC×1=Vm1/ωC,i=imsin(ωt+π2)
Therefore, alternating current i leads the alternating voltage by a phase angle of π2.The phasor diagram for the circuit between →V and →i at any instant t is shown in fig.

Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - A.L.P10videos
ALTERNATING CURRENT
- BOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - SOLVED MISCELLANEOUS14videos
ALTERNATING CURRENT
- BOOK - RESONANCECHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -3 Part-23videos
ALTERNATING CURRENT
- BOOK - RESONANCECHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
Similar Questions
Explain the term 'inductive reactance'.Show graphically the variation of inductive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied across a pure inductor L.Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of π/2.View SolutionSketch a graph showing the variation of reactance of an inductor with frequency of the applied voltage
View Solution
Knowledge Check
- Question 1 - Select One
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent l(t) leads voltage V(t) by 180∘BCurrent l(t) lags voltage V(t) by 90∘COver a full cycle the capacitor C does not consume any energy from the voltage sourceDCurrent l(t) is in phase with voltage V(t) - Question 2 - Select One
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent I(t), lags voltage V(t) by 90∘BOver a full cycle the capacitor C does not consume any energy from the voltage source.CCurrent I(t) is in phase with voltage V(t)DCurrent I(t) leads voltage V(t) by 180∘ - Question 3 - Select One
An alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
AE0ωLsin(ωt+π/2)BE0ωLsin(ωt−π/2)CE0ωLsin(ωt−π/2)DE0ωLsin(ωt+π/2)
Sketch a graph showing the variation of capacitive reactance with the change in frequency of the a.c. source.
View SolutionAn voltage, E=E0sinωt is applied acorss an inductor L. Obtain an expression for the current.
View SolutionThe alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by
View SolutionWhich one of the follwing represents the variation of capacitive reactance (XC) with the frequency (v) of the voltage source ? .
View SolutionIn a circuit containing an inductance of zero resistance, the current leads the applied a.c. voltage by a phase angle at
View Solution

