The angle made by the string of a simple pendulum with the vertical depends on time as θ=π90sin[(πs−1)t]. Find the length of the pendulum if g=π2ms−2
The correct Answer is:lenght of the pendulum is 1m.
To find the length of the pendulum given the angle made by the string with the vertical as θ=π90sin(πt−1) and g=π2m/s2, we can follow these steps:
1. Identify the angular frequency (ω):
The angle θ is given in the form θ=Asin(ωt), where A=π90 and ω=πs−1.
2. Determine the time period (T):
The angular frequency is related to the time period by the formula:
ω=2πT
Substituting ω=π:
π=2πT
Rearranging gives:
T=2s
3. Use the formula for the time period of a simple pendulum:
The time period T of a simple pendulum is given by:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
4. Substituting known values:
We know T=2s and g=π2m/s2. Substitute these values into the formula:
2=2π√Lπ2
5. Simplifying the equation:
Dividing both sides by 2:
1=π√Lπ2
This simplifies to:
1=√Lπ
6. Squaring both sides:
Squaring both sides gives:
1=Lπ
7. Solving for L:
Multiplying both sides by π:
L=πm
8. Conclusion:
The length of the pendulum is:
L=1m
Final Answer:
The length of the pendulum is L=1m.
---
The angle θ is given in the form θ=Asin(ωt), where A=π90 and ω=πs−1.
The angular frequency is related to the time period by the formula:
ω=2πT
Substituting ω=π:
π=2πT
Rearranging gives:
T=2s
The time period T of a simple pendulum is given by:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
We know T=2s and g=π2m/s2. Substitute these values into the formula:
2=2π√Lπ2
Dividing both sides by 2:
1=π√Lπ2
This simplifies to:
1=√Lπ
Squaring both sides gives:
1=Lπ
Multiplying both sides by π:
L=πm
The length of the pendulum is:
L=1m
The length of the pendulum is L=1m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Knowledge Check
The length of a simple pendulum is made one-fourth. Its time period becomes :
Afour timesBone-fourthCdoubleDhalf
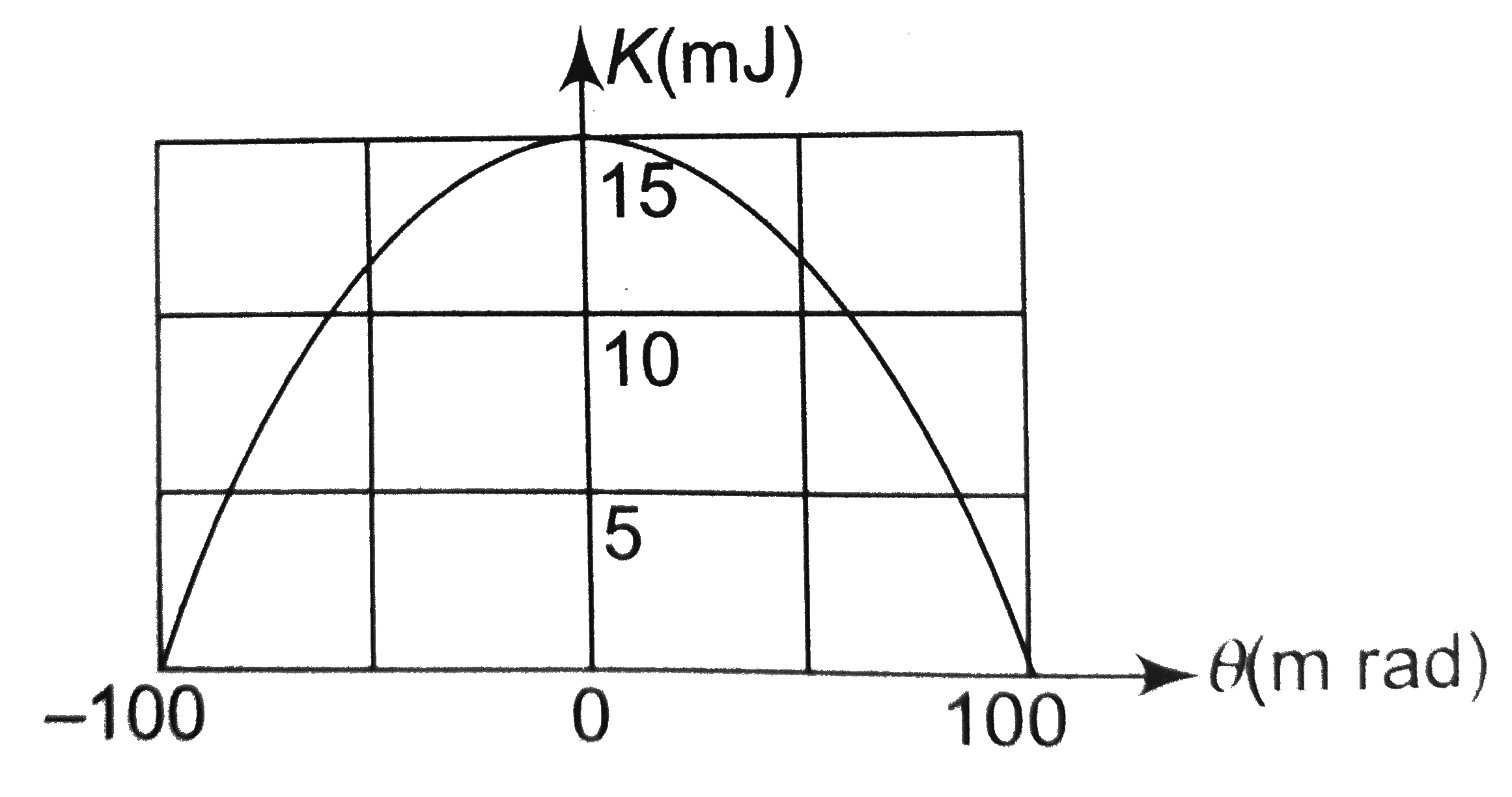
Figure shown the kinetic energy K of a pendulum versus. its angle θ from the vertical. The pendulum bob has mass 0.2kg The length of the pendulum is equal to (g=10m/s2)
,
View SolutionFind the length of seconds pendulum at a place where g=π2m/s2.
View SolutionFind the length of seconds pendulum at a place where g=4π2m/s2.
View SolutionA simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by the string of the pendulum with the vertical if this angle does not change during the turn. Take g=10ms2.
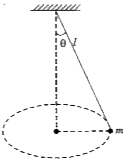
View SolutionFig. show a conical pendulum. If the length of the pendulum is l, mass of die bob is m and θ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
L=√m2gl3sin4θcosθ
View SolutionShow that the angle made by the string with the vertical in a conical pendulum is given by cosθ=gLω2 , where L is the string and ω is the angular speed.
View SolutionCalculate the time period of a simple pendulum of length one meter. The acceleration due to gravity at the place is π2ms−2.
View Solution
