Assume that a tunnel is dug across the earth (radius = R) passing through its centre . Find the time a partical takes to cover the length of the tunnel if
a. it is projected into the tunnel with a speed of √gR
b. it is released from a being R above the tunnel
c. it is thrown vertical upwards along the tunnel with a speed of √gR

The correct Answer is:A, B, C
Let M be the total mass of the earth. At any position x.
∴M1M=p×43πx3p×43πr3×x3R3
⇒M1=Mx3R3
So, force on the particle is given by
∴Fx=GMmx2
=GMmR3x.....(1)
So, acceleration of the mass 'M' at that position is given by,
ax=GMmR3
⇒axx=ω2
=GMR3=gR(g=GMR2)
So, T=2π√Rg
= time period of ocillation
(a) Now using velocity
= displacement equation
υ=ω√(A2−Y2)
[where, A = amplitude]
Given when,
y=R,υ=√gR,w=√gR
⇒√gR=√(gR)(A2−R2)
⇒R2=A2−R2
[ Now, the phases of the particle at the point
P is grater then π2 has less then π and at
Q is grater then π but less then 3π2 Let the times taken by the particle to reach the position P and Q be t1andt2 respectively, then using displacement equation].
y = r sin omega t<br>Wehave<br>R = sqrt2 R sin omega t<br>rArr omegat_1 = (3pi)/(4)<br>Wehave,R = sqrt2 R sin omega t_1<br>rArr omega t_2 = (5pi)/(4)<br>So, omega (t_2 - t_1) = (pi)/(2)<br>rArr t_2 - t_1 = (pi)/(2omega) = ((pi)/(2))/((R )/(g))<br>Timetakenbythepartic≤→travelomP→Qis<br>t_2 - t_1 = (pi)/(2) ((R )/(g))sec.<br>(b)Whenthebodyisdroppedomaheightr,thenapply∈gconservationofe≠rgy,chan≥∈P.E.=ga∈∈K.E.<br>rArr (GMm)/(R ) - (GMm).(2R) = (1)/(2) m upsilon^2<br>rArr upsilon = sqrt(gR)<br>SincethevelocityissameatP,as∈part(a)thebodywilltakensametime→travelPQ.<br>(c)WhenthebodyisprojectedverticallyupwardomPwithavelocity.(sqrt(gR)itsvelocitywillbezeroatthehighestp∮.Thevelocityofthebody,whenreachesP,aga∈wilbe<br>upsilon = sqrt((gR))
Hece the body will take same time
π2√Rg to travel P.Q.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Objective-2
Explore 15 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Objective-2
Explore 7 Videos
Similar Questions
Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.
View SolutionAssume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to reach centre of earth if it is projected into the tunnel from surface of earth with speed needed for it to escape the gravitational field to earth.
View SolutionA tunnel is made across the earth passing through its center. A ball is dropped from a height h in the tunnel. The motion will be periodic with time period::

View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
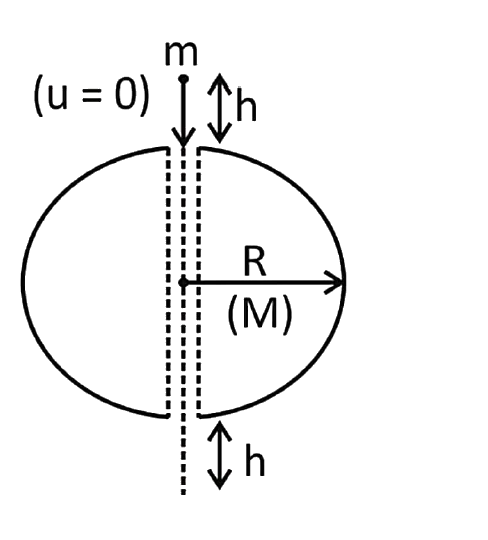
View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
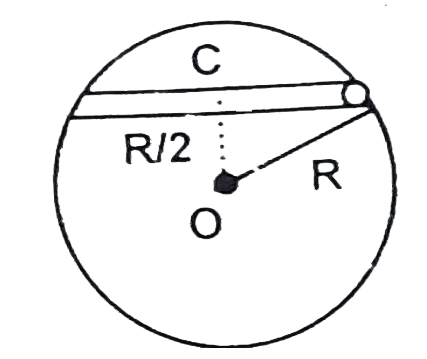
View SolutionA tunnel is dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionAssume that a tunnel is dug through earth from North pole to south pole and that the earth is a non-rotating, uniform sphere of density ρ. The gravitational force on a particle of mass m dropped into the tunnel when it reaches a distance r from the centre of earth is
View SolutionTunnel vision is caused by
View Solution