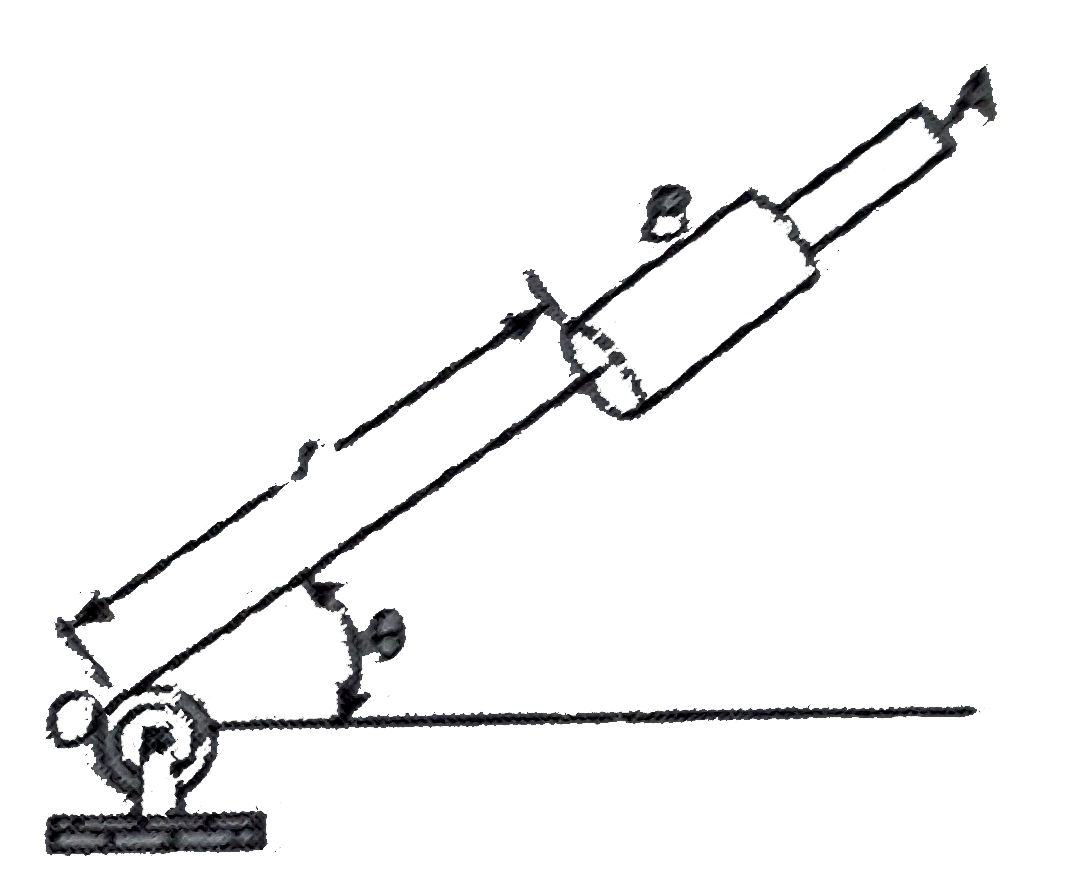
The angular displacement of the rod is defied a s0=(3)/(20) t^(2) wher

The displacement of a particle moving in a circular path is given by $θ = 3 t^{2} + 0.8,$ where $θ$ is in radian and t is in seconds . The angular velocity of the particle at t=3 sec . Is
A18 rad/s
B15 rad/s
C12 rad /s
D8 rad /s
A car moves along a straight line whose equation of motion is given by
$s = 12 t + 3 t^{2} - 2 t^{3}$
where s is in metres and t is in seconds. The velocity of the car at start will be :-
A7 m/s
B9 m/s
C12 m/s
D16 m/s
The displacement of a particle is moving by $x = {(t - 2)}^{2}$ where $x$ is in metres and $t$ in second. The distance covered by the particle in first $4$ seconds is.
A4m
B8m
C12 m
D16 m

The angular displacement of the rod is defied a s $0 = \frac{3}{20} t^{2}$ where $θ$ is in radian and t is in second. The collar B slides along the rod in such a way that its distance from O is $r = 0.9 - 0.12 t^{2}$ where r is in metre and t is secnd The velocity of collar at $θ = 30^{\circ}$ is