The angular momentum vector for a spinning wheel lies along its axle and is pointed north. To make this vector point east with chagin magnitude it is necessary to exert a force of constant magnitude on the north end of the axle in which direction?
always up
always down
at the initial moment in the east direction, but the force always remain perpendicular to the axle
always in the east direction
The correct Answer is:A
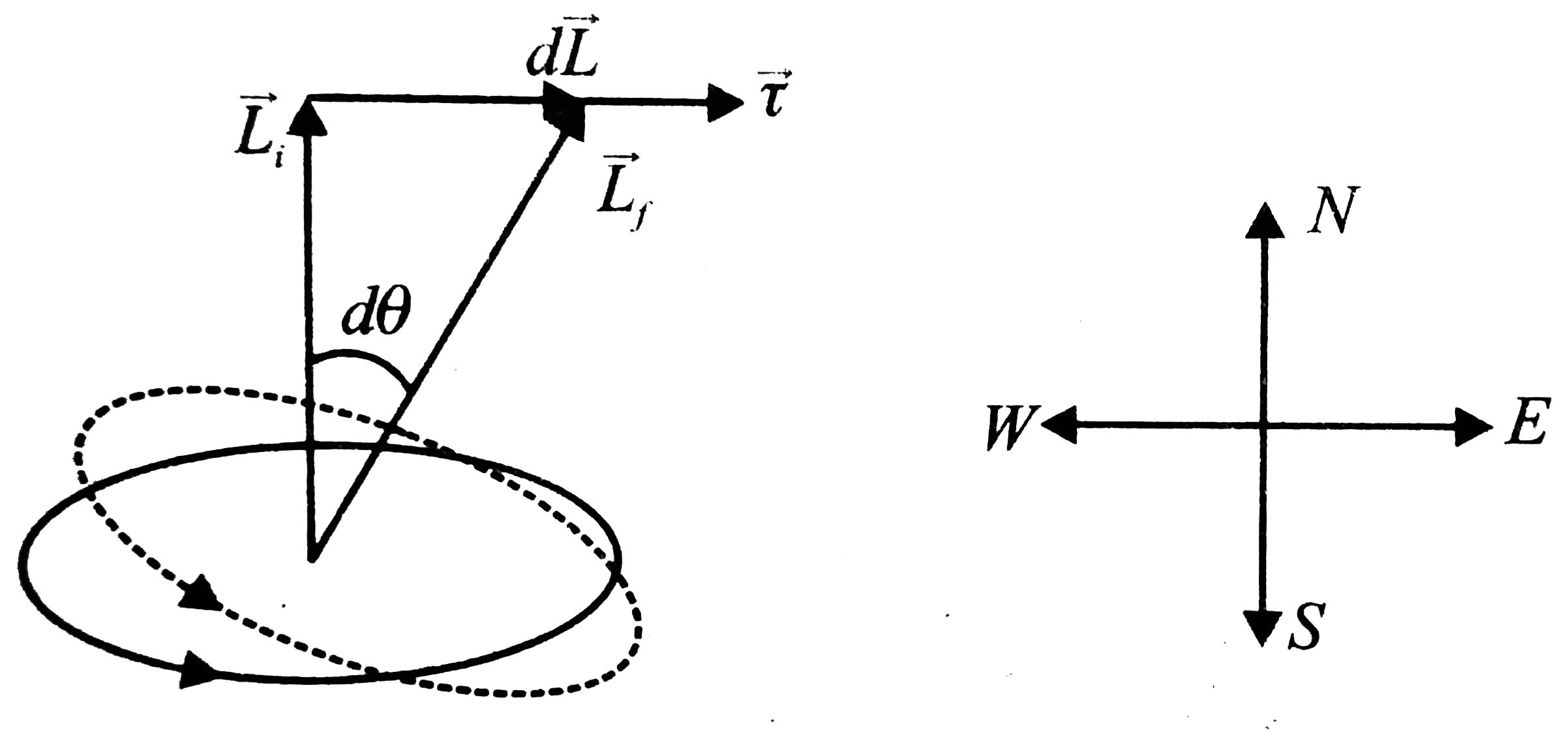
Let the wheel rotate by a small angle dθ. Then −→dL is along east, because magnitude of →L remains the same. But the torque is in the direction of change in angular momentum. So the torque should be along east. For this, the force should be in the upward direction.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
A particle lies in space at point ( 2,3,4) find the magnitude of its position vector.
View SolutionA small ball of mass m suspended from the ceiling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω. Relative to which points does the angular momentum M of the ball remain constant? Find the magnitude of the increment of the vector of the ball's angular momentum relative to the point O picked up during half a revolution.
View Solution
Knowledge Check
If a has magnitude 5 and points North-East and vector b has magnitude 5 and point North-West, then |a-b| is equal to
A25B5C7√3D5√2Displacemtn vector →A points due east and has a magnitude of 2.00km. Displacement vector →Bp∮sduenorthandhasamagnitudeof3.75Km.Displacement→−−→rvecC points due west and has a magnitude of 2.50km. Displacement vector →D points due south and has a magnitude of 3.00km. Find the magnitude and direction (relative to due west) of the resultant vector →A+→B+→C+→D.
A0.90km,56∘ north of westB0.50km,34∘ south of westC0.75k,48∘ south of westD1.25km,44∘ north of westA : The moment of force is maximum for a point if force applied on it and its position vector w.r.t. the point of rotation are perpendicular.
R : The magnitude of torque is independent of the direction of application of force.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion,BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion,CIf Assertion is true statement but Reason is false,DIf both Assertion and Reason are false statements,
The angular momentum of a particle relative to a certain point O varies with time as M=a+bt2, where a and b are constant vectors, with a⊥b. Find the force moment N relative to the point O acting on the particle when the angle between the vectors N and M equals 45∘.
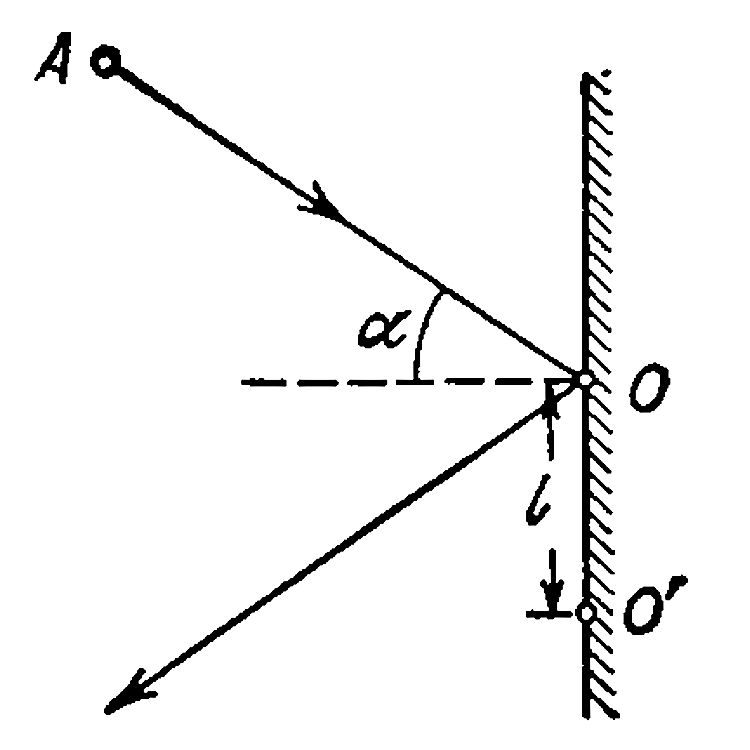
View SolutionA disc A of mass m sliding over a smooth horizontal surface with velocity v experiences a perfectly elastic collision with a smooth stationary wall at a point O (figure). The angle between the motion direction of the disc and the normal of the wall is equal to α. Find:
(a) the points relative to which the angular momentum M of the disc remains constant in this process,
(b) the magnitude of the increment of the vector of the disc's angular momentum relative to the point O′ which is located in the plane of the disc's motion at the distance l from the point O.
View Solution50 A current in north to south direction. Give the magnitude and direction of →B at a point2.5 m east of the wire.
View SolutionAt a harbour, a boat is standing and wind is blowing at a speed of √2m/sec. due to which , the flag on the boat flutters along north− east. Now the boat enters in to river, which is flowing with a velocity of 2m/sec. Due north. The boat starts with zero velocity relative to the river and its constant acceleration relative to the river is 0.2m/sec2 due east. In which direction will the flag flutter at 10 seconds ?
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
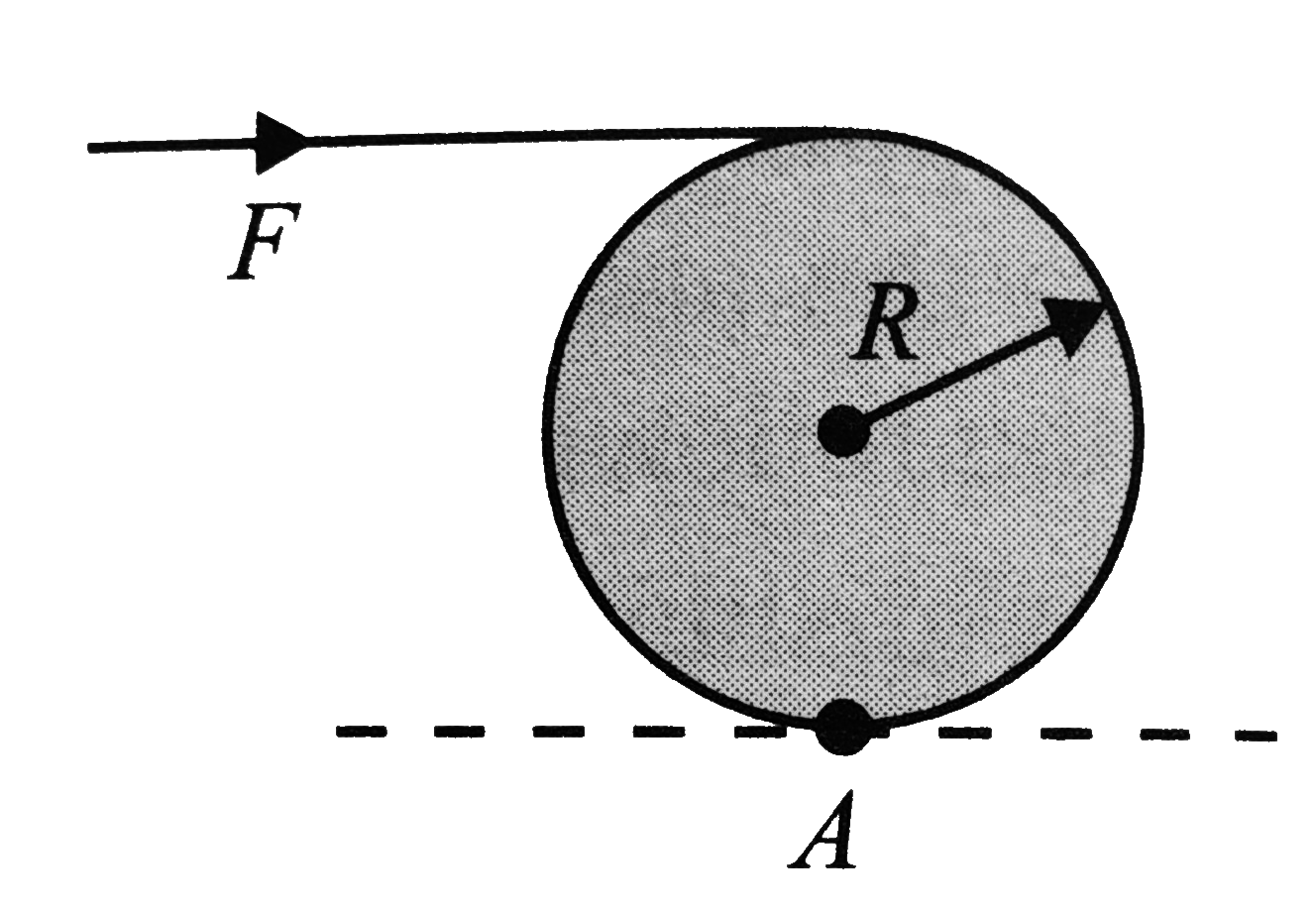
Component of reaction at the hinge in the vertical direction is
View Solution
