The angular momentum vector for a spinning wheel lies along its axle and is pointed north. To make this vector point east with chagin magnitude it is necessary to exert a force of constant magnitude on the north end of the axle in which direction?
always up
always down
at the initial moment in the east direction, but the force always remain perpendicular to the axle
always in the east direction
The correct Answer is:A
To solve the problem, we need to understand how to change the direction of the angular momentum vector of the spinning wheel from pointing north to pointing east. We will use the right-hand rule to determine the direction of the torque required to achieve this change.
1. Identify the Initial Angular Momentum Direction:
The angular momentum vector →L of the spinning wheel is initially directed north.
2. Determine the Desired Angular Momentum Direction:
We want to change the direction of →L so that it points east.
3. Understand the Relationship Between Torque and Angular Momentum:
The torque →τ is related to the change in angular momentum by the equation:
→τ=d→Ldt
This means that a torque must be applied to change the angular momentum vector.
4. Apply the Right-Hand Rule:
To find the direction of the torque, we can use the right-hand rule. Point your thumb in the direction of the initial angular momentum (north) and then curl your fingers in the direction of the desired change (from north to east).
5. Visualize the Rotation:
As you rotate your wrist from north to east, your fingers will curl upwards. This indicates that the torque must be directed upwards.
6. Conclusion:
Therefore, to change the angular momentum vector from pointing north to pointing east, a force must be applied at the north end of the axle in the upward direction.
Final Answer:
The direction of the force exerted on the north end of the axle must be upward.
---
The angular momentum vector →L of the spinning wheel is initially directed north.
We want to change the direction of →L so that it points east.
The torque →τ is related to the change in angular momentum by the equation:
→τ=d→Ldt
This means that a torque must be applied to change the angular momentum vector.
To find the direction of the torque, we can use the right-hand rule. Point your thumb in the direction of the initial angular momentum (north) and then curl your fingers in the direction of the desired change (from north to east).
As you rotate your wrist from north to east, your fingers will curl upwards. This indicates that the torque must be directed upwards.
Therefore, to change the angular momentum vector from pointing north to pointing east, a force must be applied at the north end of the axle in the upward direction.
The direction of the force exerted on the north end of the axle must be upward.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
Knowledge Check
A long straight wire in the horizontal plane carries as curret of 75 A in north to south direction, magnitude and direction of field B at a point 3 m east of the wire is
A4×10−6T, vertical upB5×10−6T, vertical downC5×10−6T, vertical upD4×10−6T, vertical down
A rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration

A. the normal reaction on the bead will be constant h magnitude and direction both
B. the magnitude of the normal reaction on the bead will be variable
C. the magnitude of friction force on the bead will be constant
D. the magnitude of friction force on the bead will be variable
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as

View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
The limiting electric potential of the sphere is
View SolutionA : The moment of force is maximum for a point if force applied on it and its position vector w.r.t. the point of rotation are perpendicular.
R : The magnitude of torque is independent of the direction of application of force.
View SolutionAt a harbour, a boat is standing and wind is blowing at a speed of √2m/sec. due to which , the flag on the boat flutters along north− east. Now the boat enters in to river, which is flowing with a velocity of 2m/sec. Due north. The boat starts with zero velocity relative to the river and its constant acceleration relative to the river is 0.2m/sec2 due east. In which direction will the flag flutter at 10 seconds ?
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
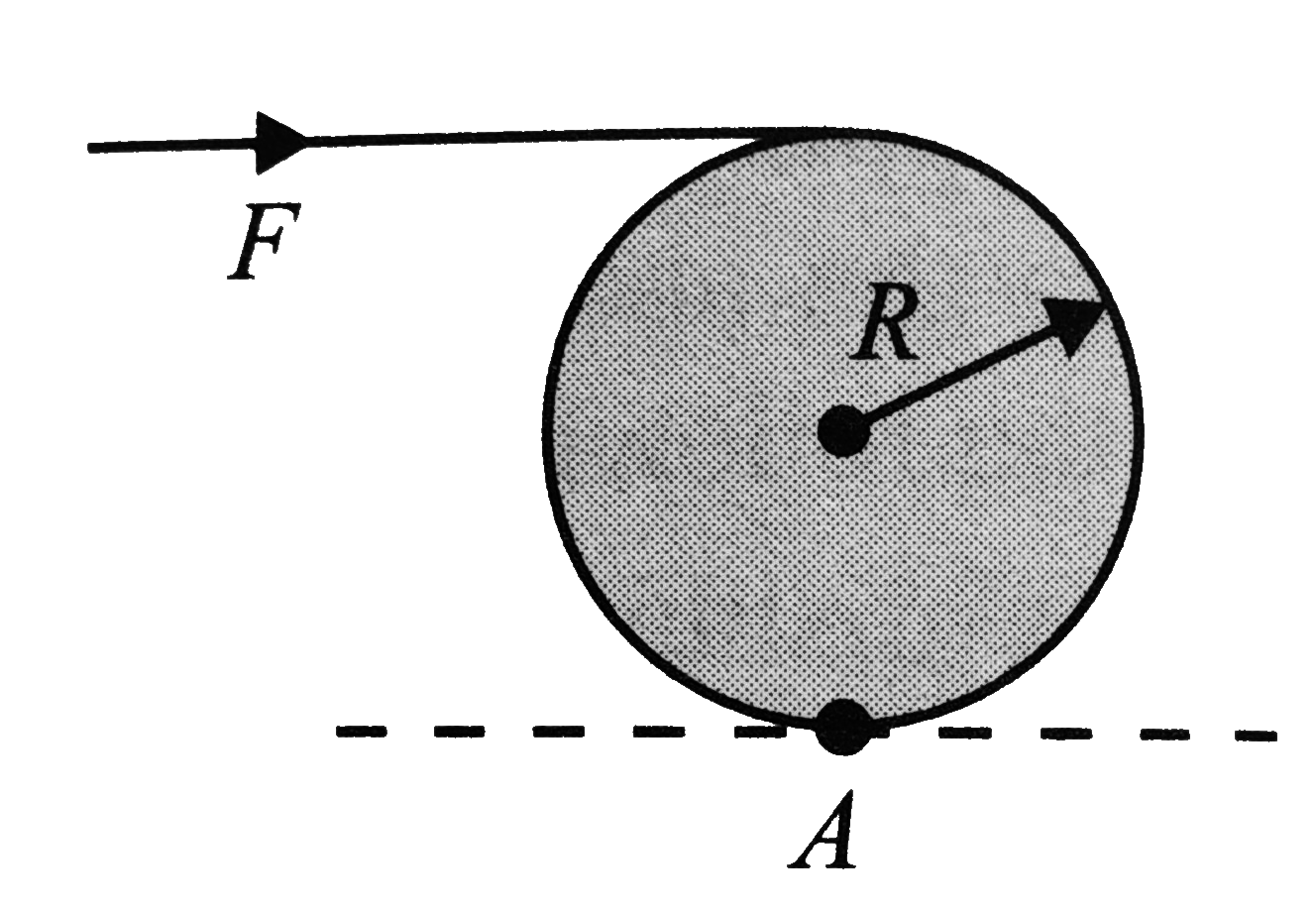
Component of reaction at the hinge in the vertical direction is
View SolutionAn electromagnetic wave propagating along north has its electric field vector upwards. Its magnetic field vector point towards
View Solution
