A particle lies in space at point ( 2,3,4) find the magnitude of its position vector.
The correct Answer is:√29
To find the magnitude of the position vector of a particle located at the point (2, 3, 4), we can follow these steps:
1. Identify the Position Vector:
The position vector →OA of a point A(x,y,z) in space with respect to the origin O(0,0,0) can be expressed as:
→OA=x^i+y^j+z^k
For the point (2, 3, 4), we have:
→OA=2^i+3^j+4^k
2. Calculate the Magnitude of the Position Vector:
The magnitude of a vector →A=a^i+b^j+c^k is given by the formula:
|→A|=√a2+b2+c2
Here, a=2, b=3, and c=4. Therefore, we calculate:
|→OA|=√22+32+42
3. Perform the Squaring:
Calculate each square:
22=4,32=9,42=16
4. Sum the Squares:
Now, add these squared values:
4+9+16=29
5. Take the Square Root:
Finally, take the square root of the sum:
|→OA|=√29
6. Approximate the Value:
The approximate value of √29 is about:
|→OA|≈5.38
Final Answer:
The magnitude of the position vector is √29 or approximately 5.38.
The position vector →OA of a point A(x,y,z) in space with respect to the origin O(0,0,0) can be expressed as:
→OA=x^i+y^j+z^k
For the point (2, 3, 4), we have:
→OA=2^i+3^j+4^k
The magnitude of a vector →A=a^i+b^j+c^k is given by the formula:
|→A|=√a2+b2+c2
Here, a=2, b=3, and c=4. Therefore, we calculate:
|→OA|=√22+32+42
Calculate each square:
22=4,32=9,42=16
Now, add these squared values:
4+9+16=29
Finally, take the square root of the sum:
|→OA|=√29
The approximate value of √29 is about:
|→OA|≈5.38
The magnitude of the position vector is √29 or approximately 5.38.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -B Objective (one option is correct)
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Knowledge Check
The point (-2,-3,-4) lies in the
Afirst octantBseventh octantCsecond octantDeighth octant
A particle executies linear simple harmonic motion with an amplitude 3cm .When the particle is at 2cm from the mean position , the magnitude of its velocity is equal to that of acceleration .The its time period in seconds is
View SolutionA particle executes linear simple harmonic motion with an amplitude of 3cm. When the particle is at 2cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then, its time period in seconds is
View SolutionA particle excutes simple harmonic motion with an amplitude of 5 cm. When the particle is at 4 cm from the mean position, the magnitude of its velocity in SI units is equal to that of its acceleration. Then, its periodic time in seconds is
View SolutionA particle moves in xy-plane from position (1m,2m) to (3m,4m) in 2s. Find the magnitude and direction of average velocity.
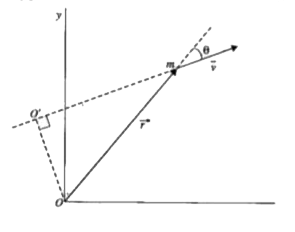
View SolutionA point mass 10 g moves in the xy plane with a velocity 2ms−1 along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector →r is 0.5 m and the angle θ=30∘.
View SolutionPosition of a particle in a rectangular -co-ordinate (3,2,5). Then its position vector will be
View SolutionPosition of a particle in a rectangular -co-ordinate (3,2,5). Then its position vector will be
View Solution
