The arrangement shown below consists of a uniform metre scale of length 1 m, balanced on a fixed hemisphere of radius 20 cm. when one end of the scale is slightly pressed and released, it performs S.H.M. Determine the angular frequency of oscillations.
(Take g = 10 ms−2)
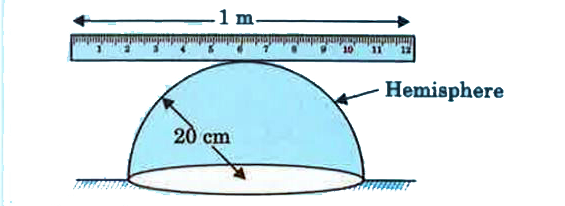
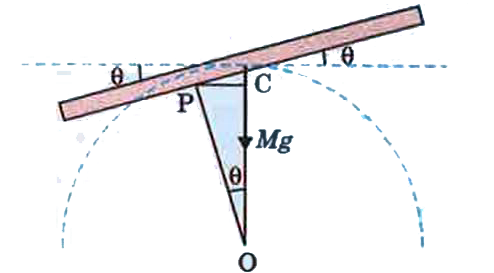
Let θ be the angle be which the rod is pressed. The restoring forc on the rod will be its weight, acting downwards at C.
The magnitude of the restoring torque = force × perpendicular distance =Mg×CP=Mg×OPsinθ=mg×Rsinθ (where) OP = R = radius of sphere).
Since θ is small so sinθ=θ where θ is in radains, IF I is the moment of inertia of the rod. then the equations of motion of the scale is
Id2θdt2=mgRθ
or d2θdt2=(−mgRI)θ {negative sign due to restoring nature.}
Thus, the motion is simple haromonic with angular frequency
ω2=(MgRI)
⇒ω=√MgRI(∵ML212)
∴ω=√12gRL2
Using the values L = 1m, g = 10 ms−2 and R = 0.2 m, we get = 4.898 rad/s.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT FILE (Textbook Exercises)
19 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT (Additional Exercises)
6 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Conceptual Questions
18 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
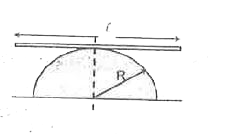
A uniform plank of length l and mass m is balanced on a fixed semi-circular plate of radius R as shown in the figure. If the plank is tilted slightly from its equilibrium position, and released, prove that it will execute S.H.M find the period of its oscillation.
View SolutionA vertical U-tube contains liquid of uniform density upto a height of 3 cm. If the liquid in one arm is depressed and then released, it performs S.H.M. in the tube. Calculate its time period of oscillations.
Assume U-tube to be of uniform cross section.
Take, g = 980 cm/s2
View Solution
Knowledge Check
A pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
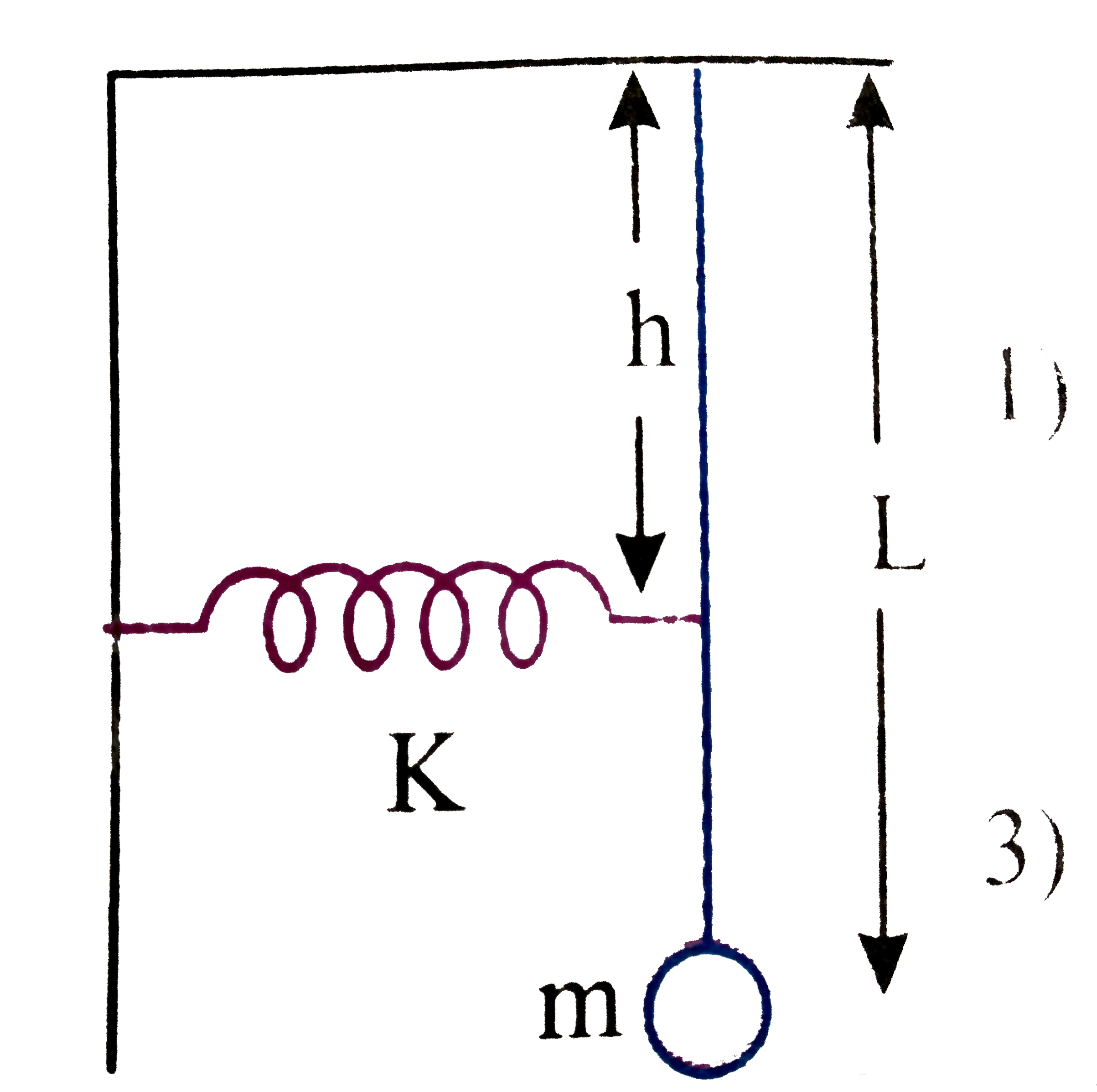 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2A spring balance has a scale that reads from 0 to 50 kg. the length of the scale is 20 cm. a block of mass m is suspended from this balance, when displaced and released, it oscillates with a period 0.5 s. the value of m is (Take g=10ms−2)
A8 kgB12 kgC16 kgD20 kgA uniform meter scale balances at the 40 cm mark when weights of 10g and 20g are suspended from the 10cm and 20cm marks. The weight of the metre scale is
A50 gB60 gC70 gD80 g
Two springs of spring constant mgl each are attached to the end of a uniform rod of mass m and length l=1.25m which is hinged in vertical plane as shown in figure. As the rod is rotated slightly about the hinge, it undergoes SHM with angular frequency ω. Find ω (in rad/s). (Take g=10ms2)
'(##CEN_KSR_PHY_JEE_C16_E01_013_Q04##)'
View SolutionAn arrangement of three identical spring and a block of mass 10 kg is shown in the adjoining figure. When the platform on which block is placed is slightly pressed down and released. It performs S.H.M. with a period of 2 s.
(i) Calculate the spring constant of the spring.
(ii) If a block of mass m is further placed on the platform, the new period of S.H.M. becomes 3.5 s. Find the value of m. (Assume platform to be massless)

View SolutionA thin vertical tube of weight 12 g and external diameter 1 cm is made to float vertically in water by placing 12 g of mercury at its bottom. If the tube is depressed slightly and then released, determine the time period of S.H.M.
Take g=10m/s2
View SolutionA spring balance has a scale that reads from 0 to 50 kg. the length of the scale is 20 cm. a block of mass m is suspended from this balance, when displaced annd released, it oscillates with a period 0.5 s. the value of m is (Take g=10ms−2)
View SolutionA uniform meter scale balance s at the 40-cm mark when weihgt of 10g and 20g are suspended from the 10-cm and 20-cm marks respectively. The weight of the meter scale is
View Solution
