The block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block
For the motion of block m:

Along horizontal direction , N1=ma
Along vertical direction mg−(μ1N1+T)=m(2a)
After substituting value of N1 in fig (i) , we have
Mg−(μ1ma+T)=m(2a)
For the motion of block M:
Along verticle direction ∑Fv=0
or N2=T+μ1N1+Mg
Along horizontal direction
2T−(N1+μ2N2)=Ma
From equation (i) and (iii) we get
2T−[N1+μ2(T+μ1N1+Mg)]=Ma
or 2T−[ma+μ2u2(ma)+μ2Mg]=Ma...(v)
Now solving equation(ii) and (iv) , we get
a=2m−μ2(M+m)gM+m(5+2(μ1−μ2)]
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
For the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is
 AF2m−2μgBF2mCF2m−μgDzero
AF2m−2μgBF2mCF2m−μgDzeroConsider the situation as shown in the diagram.
The coefficient of friction between the block is 0.5. The acceleration of the lower block isA1m/s2B1.5m/s2C2m/s2D2.5m/s2Two blocks M and m are arranged as shown in the diagram The coefficient of friction between the block is μ1=0.25 and between the ground and M is μ2=13 If M=8kg then find the value of m so that the system will remain at rest
 A4/3kgB8/9kgC1kgD8/5kg
A4/3kgB8/9kgC1kgD8/5kg
Two blocks of masses 'm' and and 'M' are arranged as shown in the The coefficient of friction between the two blocks is 'μ', where as between the lower block and the horizontal surface is zero. Find the force 'F' to be applied on the upper block for the system to be under equilibrium ? .

View SolutionA small block of mass m is projected on a larger block of mass 10m and length l with a velocity v as shown in the figure. The coefficient of friction between the two block is μ2 while that between the lower block and the ground is μ1. Given that μ2>11μ1.

(a) Find the minimum value of v, such that the mass m falls off the block of mass 10m .
(b) If v has minimum value, find the time taken by block m to do so.
View SolutionConsider the situation as shown in the figgure. The coefficent of friction between the blocks is μ. Find the acceleration of each block.

View SolutionIn the figure shown coefficient of friction between block A and ground is 0.4 and that between wedge and block B is zero. Wedge is fixed. Find tension is string and acceleration of block A if F = 28 N.

View SolutionTwo blocks of masses m and 2 m are placed one over the other as shown in figure.The coefficient of friction between m and 2m is μ and between 2m and ground is μ3. If a horizontal force F is applied on upper block and T is tension developed in string, then choose the incorrect alternative.
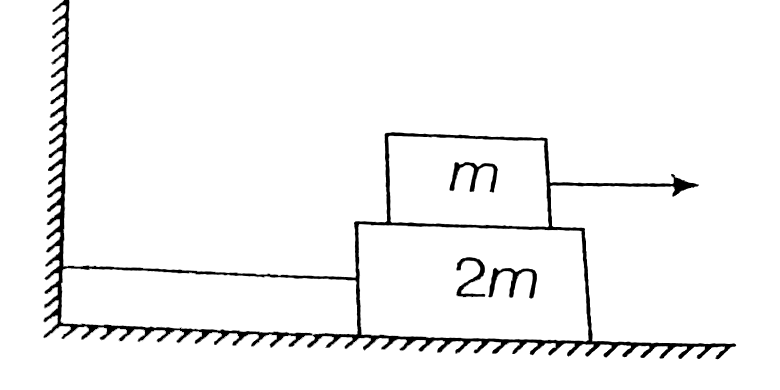
View Solution
