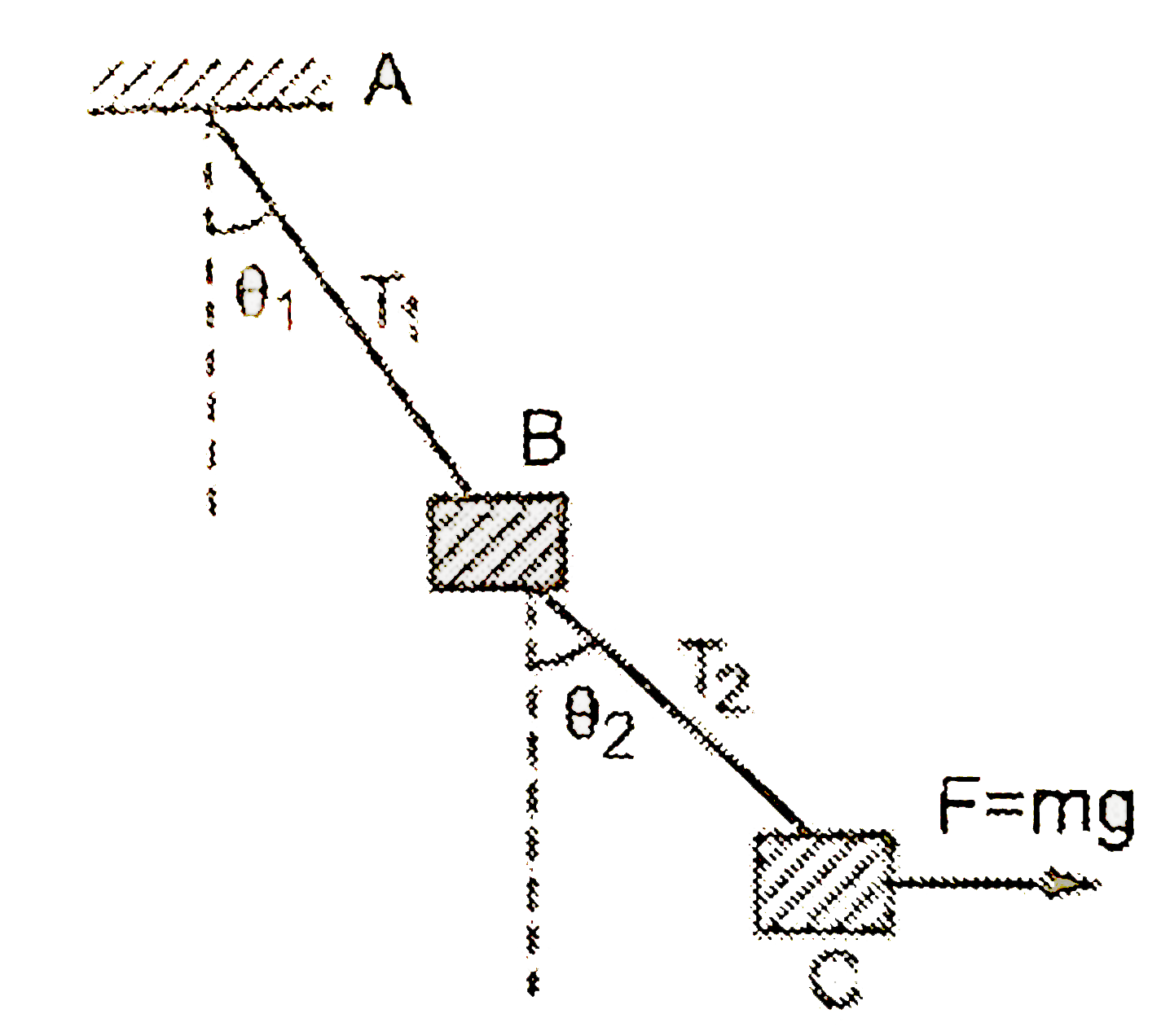
The blocks B and C in the figure have mass m each. The strings AB and BC are light, having tensions T1 and T2 respectively. The system is in equilibrium with a constant horizontal force mg acting on C.
tanθ1=1/2
tanθ2=1
T1=√5mg
T2=√2mg
The correct Answer is:A, B, C, D
Step by step video, text & image solution for The blocks B and C in the figure have mass m each. The strings AB and BC are light, having tensions T_(1) and T_(2) respectively. The system is in equilibrium with a constant horizontal force mg acting on C. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Type 2
22 Videos
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Revision Exercise
26 Videos
- IIT QUESTIONS 5BOOK - D MUKHERJEECHAPTER - IIT QUESTIONS 5EXERCISE - Matrix matching type
2 Videos
- MISCELLANEOUS QUESTION 1BOOK - D MUKHERJEECHAPTER - MISCELLANEOUS QUESTION 1EXERCISE - Miscellaneous Questions-1 (Straight-Objective Type)
54 Videos
Similar Questions
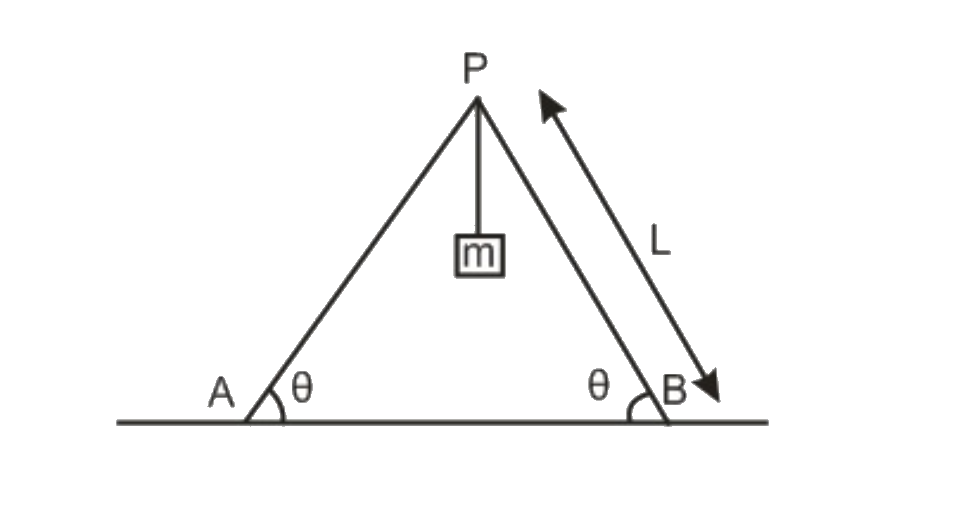
Two identical ladders are arranged as shown in the figure. Mass of the block is m and the mass of each ladder is M. The length of each of the ladder is L. The system is in equilibrium. What is the magnitude of frictional force acting at A or B?
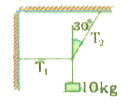
View SolutionA block of mass 10 kg is suspended with two strings as shown in the fig. Find the tensions T1andT2 in the two string.
View Solution
Knowledge Check
The blocks B and C in the figure have mass m each. The strings AB and BC are light having tension T1 and T2 respectively. The system is in equilibrium with a constant horizontal forcemg acting on C. Then which one is incorrect.
 Atanθ1=12Btanθ=1CT1=√5mgDT2=mg
Atanθ1=12Btanθ=1CT1=√5mgDT2=mgFigure, represents a light inextensible string ABCDE in which AB=BC=CD=DE and to which are attached masses M,m, and M at the point B,C and D, respectively. The system hangs freely in equilibrium with ends A and E of the string fixed in the same horizontal line. it is given that tanα=3/4 and tanβ=12/5. Then the tension in the string BC is
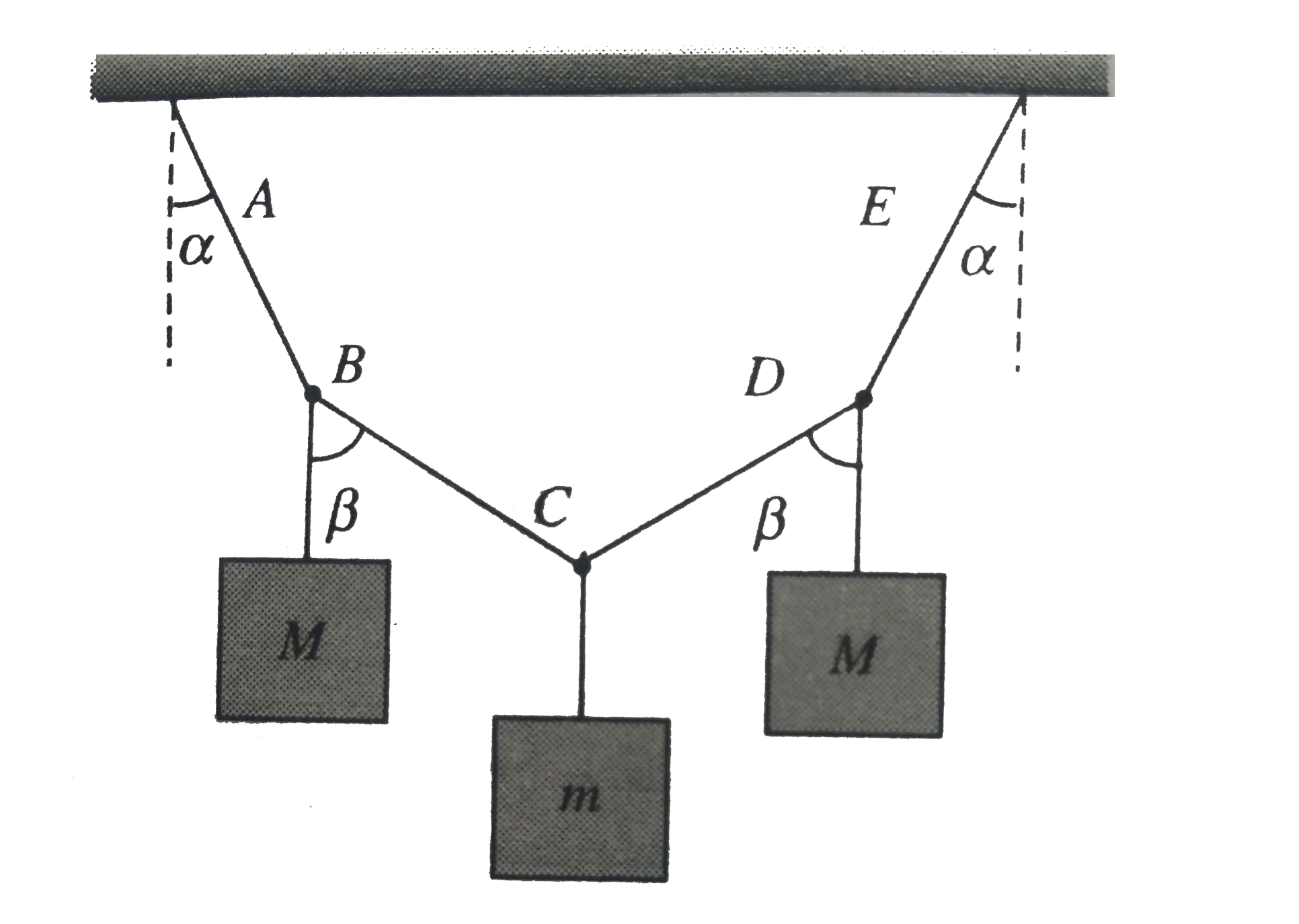 A2mgB(13/10)mgC(3/10)mgD(20/11)mg
A2mgB(13/10)mgC(3/10)mgD(20/11)mgIn the figure, the blocks A,B and C of mass m each have accelerations a1,a2 and a3 respectively. F1 and F2 are external forces of magnitude 2mg and mg respectively.
 Aa1=a2=a3Ba1>a3>a2Ca1=a2,a2>a3Da1>a2,a2=a3
Aa1=a2=a3Ba1>a3>a2Ca1=a2,a2>a3Da1>a2,a2=a3
Three blocks are placed as shown in figure. Mass of A, B and C are m1,m2,and m3respectively. The force exerted by block 'C' on 'B' is :-
View SolutionIn the system shown, the blocks A,B and C are of weight 4W, W and W respectively. The system set free. The tension in the string connecting the blocks B and C is

View SolutionIn the system shown in fig., block A and C are placed on smooth floors and both have mass equal to m1. Blocks B and D are identical having mass m2 each. Coefficient of friction
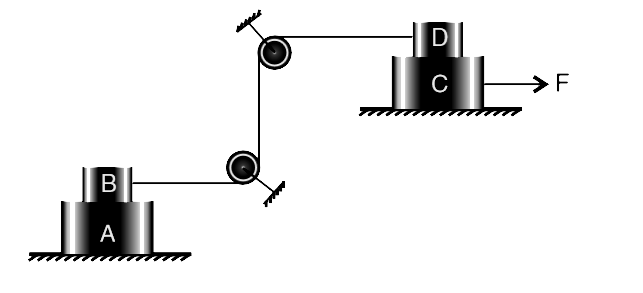
Between A and B and that between C and D are both equal to μ. String and pulleys are light. A horizontal force F is applied on block C and is gradually increased.
(a) Find the maximum value of F (call it F0) so that all the four blocks move with same acceleration.
(b) Will the value of F0 increase or decrease if another block (E) of mass m2 is placed above block D and coefficient of friction between E and D is μ?
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
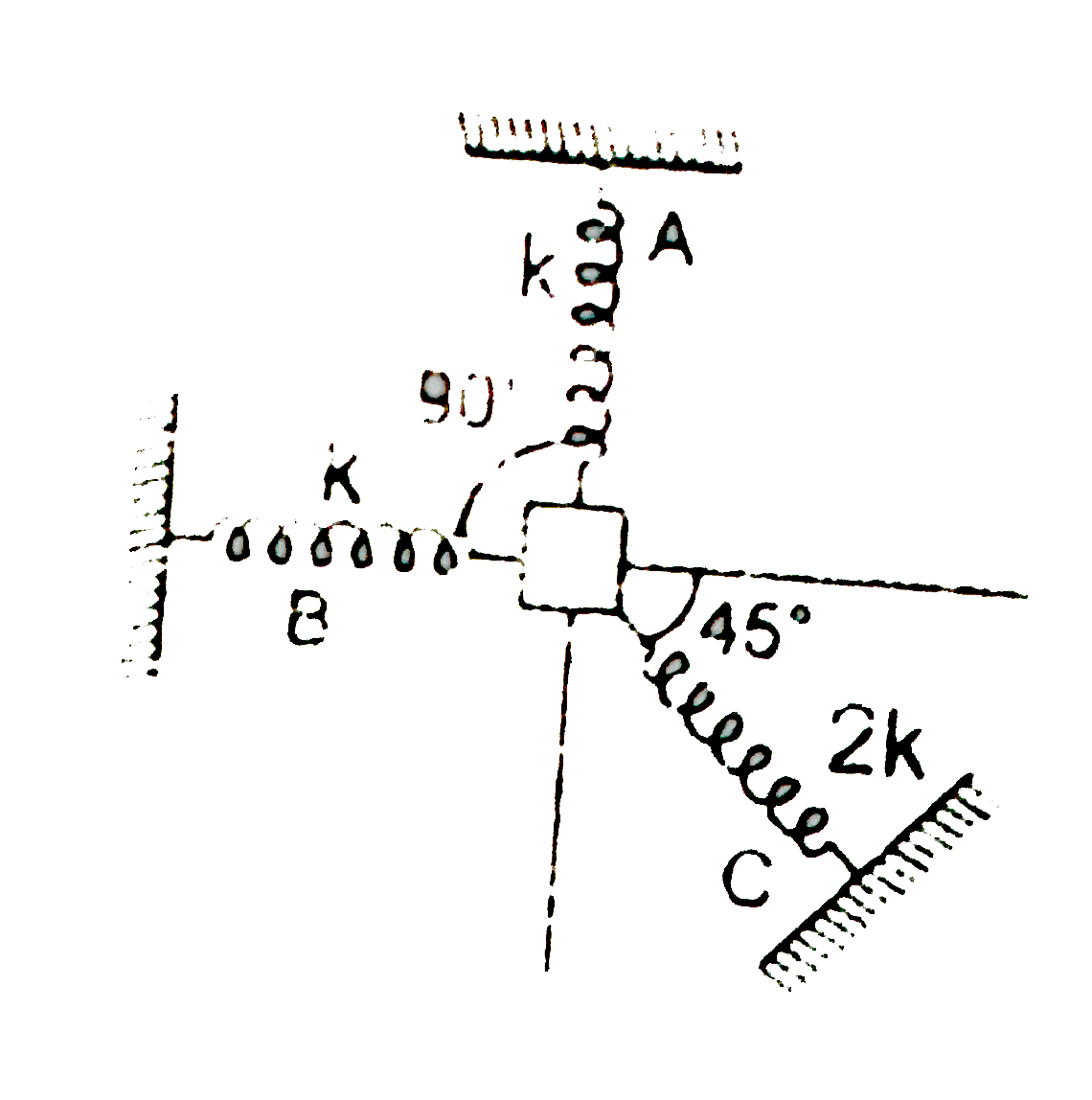
View SolutionBlock A of mass m and block B of mass 2m are placed on a fixed triangular wedge by means of a light and inextensible string and a frictionless pulley as shown in fig . The wedge is inclined at 45∘ to the horizontal on both sides . The coefficient of friction between the block Aand the wedge is 2/3 and that between the block B and the wedge is 1/3 .If the system of AandB is released from rest then find .
a. the acceleration of A
b. tension in the string
c.the magnitude and direction of the frictional force acting on A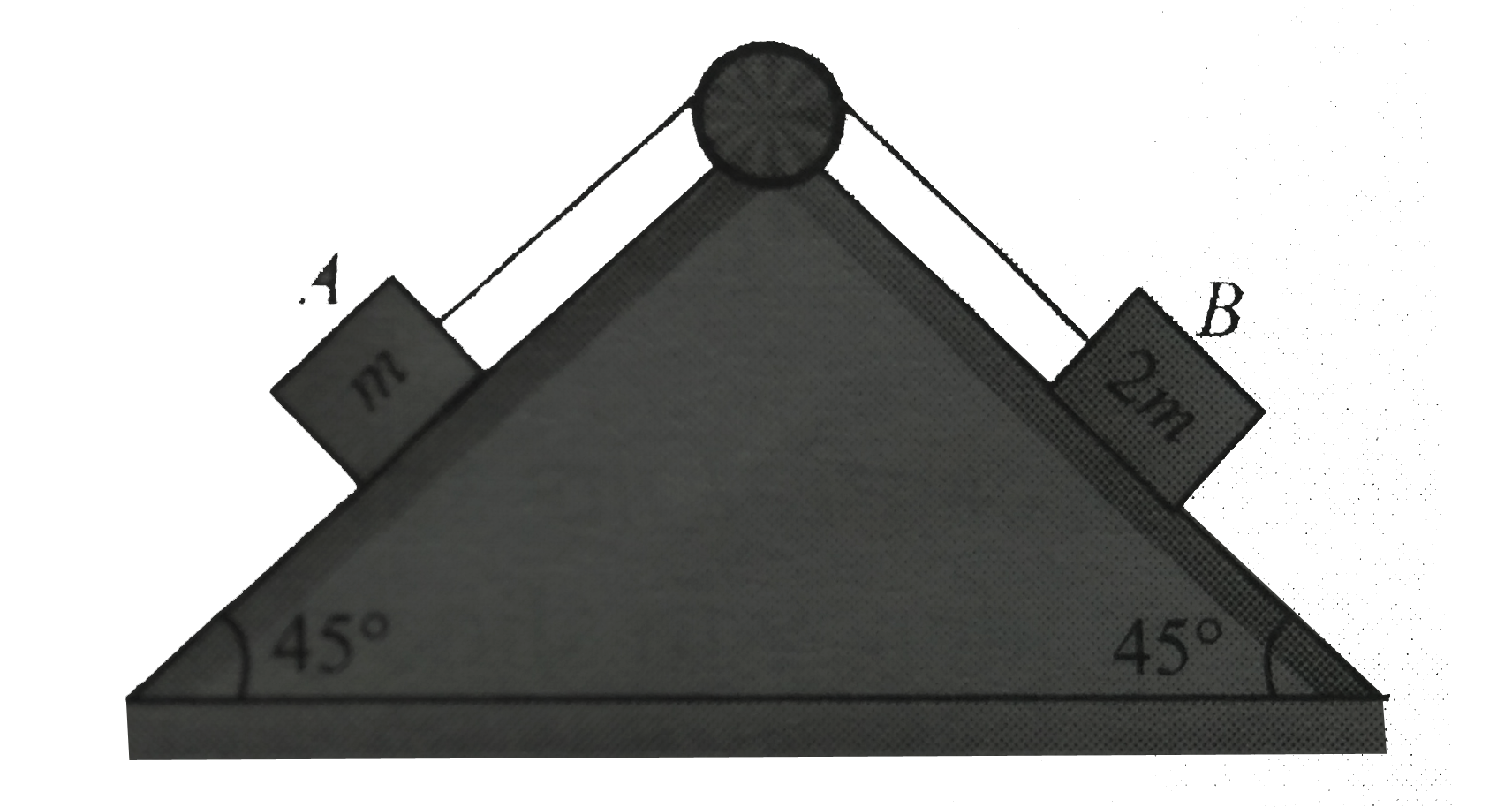
View Solution
