A small body b starts from rest at the hightest point A of a large fixed sphere , with centre C ,and slides down with a small but constant speed , then ,the coefficent of friction between B and the sphere ,at any point P on the surface of the sphere such that
must be equal to
The correct Answer is:C
Step by step video, text & image solution for A small body b starts from rest at the hightest point A of a large fixed sphere , with centre C ,and slides down with a small but constant speed , then ,the coefficent of friction between B and the sphere ,at any point P on the surface of the sphere such that angle ACP=theta, must be equal to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS, FORCESBook:D MUKHERJEEChapter:KINEMATICS, FORCESExercise:Type 2
Explore 22 Videos
- IIT QUESTIONS 5Book:D MUKHERJEEChapter:IIT QUESTIONS 5Exercise:Matrix matching type
Explore 2 Videos
- MISCELLANEOUS QUESTION 1Book:D MUKHERJEEChapter:MISCELLANEOUS QUESTION 1Exercise:Miscellaneous Questions-1 (Straight-Objective Type)
Explore 54 Videos
Similar Questions
A point A on a sphere of weight w rests in contact with a smooth vertical wall and is supported by a string joining a point B on the sphere to a point C on the wall. Draw free body diagrame of the spheres.

View SolutionA point mass m starts to slide from rest from the top of a smooth solid sphere of radius r. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and sphere, does the mass fly off at a greater or lesser angle ?
View Solution
Knowledge Check
A solid sphere starts from rest at the top of an incline of height h and length l, and moves down. The force of friction between the sphere and the incline is F. This is insufficient to prevent slipping. The kinetic energy of the sphere at the bottom of the incline is W.
AThe work done against the force of friction is Fl.BThe heat produced is Fl.CW=mgh-FlDW>(mgh-Fl)A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The smallest kinetic energy at the bottom of the incline will be achieved by
Athe work done against the frictional force is Fl.Bthe heat produced is F l.CW = mgh - F lDW gt (mgh - F l)State of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.

What will be the speed of sphere when it starts pure rolling?A4u7B3u7C2u7Du7
A sphere of radius a subtends an angle 60∘ at a point P. Then the distance of P from the centre of the sphere is.
View SolutionA small body A starts sliding down from the top of a wedge (see fig) whose base is equal to l. The coefficient of friction between the body and wedge surface is μ=1.0. At what value of angle q will the time of sliding be least?
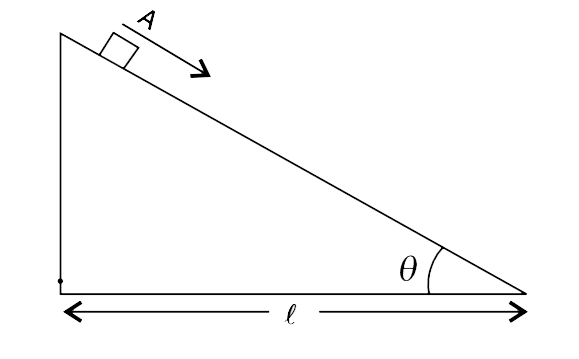
View SolutionA particle slides down the surface of a smooth fixed sphere of radius R starting from rest at the highest point B. Particle leaves the sphere at some point and then strikes the horizontal plane passing through the lowest point A of the sphere at point P. The distance AP is given by
AP=n27[√n+4√2]R where 'n' is an integer, find n (Take g=10m/s2)

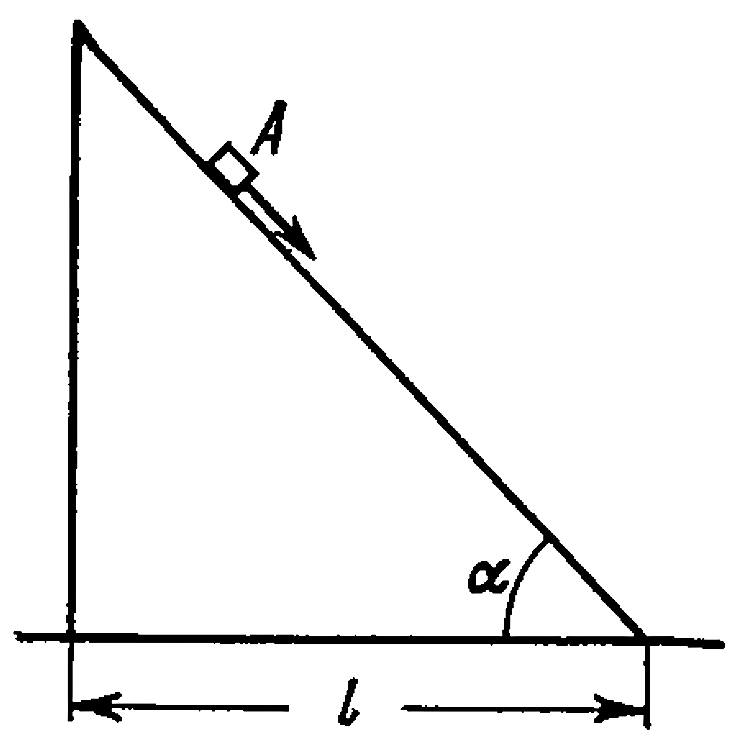
View SolutionA small body A starts sliding down from the top of a wedge (figure) whose base is equal to l=2.10m. The coefficient of friction between the body and the wedge surface is k=0.140. At what value of the angle α will the time of sliding be the least? What will it be equal to?
View SolutionA small disk of mass m lies on the highest point of a sphere of radius R. A slight push makes the disk start sliding down. Find the force of pressure of the disk on the sphere as a function of the angle its radius vector makes with the vertical. Where does the disk lose contact with the sphere? Friction is to be neglected.
View Solution