The bob of a pendulum is moving with a speed of 5 m/s while passing through mean position . Calculate its speed at the position when it makes an angle of 30∘ with the vertical . The length of pendulum is 0.6 m / Use g=10m/s2
To solve the problem, we will use the principle of conservation of mechanical energy. The total mechanical energy (kinetic + potential) at the mean position will be equal to the total mechanical energy at the position where the pendulum makes an angle of 30 degrees with the vertical.
1. Identify the initial conditions:
- Speed at the mean position (v_initial) = 5 m/s
- Length of the pendulum (L) = 0.6 m
- Angle with vertical (θ) = 30 degrees
- Acceleration due to gravity (g) = 10 m/s²
2. Calculate the initial kinetic energy (KE_initial):
KEinitial=12mv2initial=12m(5)2=252m
3. Calculate the potential energy (PE_initial) at the mean position:
PEinitial=0(since height is zero at the mean position)
4. Calculate the height (h) when the pendulum makes an angle of 30 degrees:
- The height can be calculated using the formula:
h=L−Lcos(θ)=L(1−cos(θ))
- For θ = 30 degrees, cos(30∘)=√32:
h=0.6(1−√32)=0.6(1−0.866)=0.6×0.134=0.0804m
5. Calculate the potential energy (PE_final) at the angle of 30 degrees:
PEfinal=mgh=mg(0.0804)=m⋅10⋅0.0804=0.804m
6. Set up the conservation of energy equation:
KEinitial+PEinitial=KEfinal+PEfinal
252m+0=12mv2final+0.804m
7. Cancel the mass (m) from the equation:
252=12v2final+0.804
8. Rearrange to solve for v2final:
252−0.804=12v2final
252−1.6082=12v2final
25−1.6082=12v2final
23.3922=12v2final
23.392=v2final
9. Calculate vfinal:
vfinal=√23.392≈4.83m/s
Final Answer:
The speed of the pendulum bob at an angle of 30 degrees with the vertical is approximately 4.83 m/s.
- Speed at the mean position (v_initial) = 5 m/s
- Length of the pendulum (L) = 0.6 m
- Angle with vertical (θ) = 30 degrees
- Acceleration due to gravity (g) = 10 m/s²
KEinitial=12mv2initial=12m(5)2=252m
PEinitial=0(since height is zero at the mean position)
- The height can be calculated using the formula:
h=L−Lcos(θ)=L(1−cos(θ))
- For θ = 30 degrees, cos(30∘)=√32:
h=0.6(1−√32)=0.6(1−0.866)=0.6×0.134=0.0804m
PEfinal=mgh=mg(0.0804)=m⋅10⋅0.0804=0.804m
KEinitial+PEinitial=KEfinal+PEfinal
252m+0=12mv2final+0.804m
252=12v2final+0.804
252−0.804=12v2final
252−1.6082=12v2final
25−1.6082=12v2final
23.3922=12v2final
23.392=v2final
vfinal=√23.392≈4.83m/s
The speed of the pendulum bob at an angle of 30 degrees with the vertical is approximately 4.83 m/s.
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (A. Multiple Choice Questions)
29 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (B. Multiple Choice Questions)
46 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Revision Exercise (Long Answer Questions)
9 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A pendulum bob has a speed 3m/s while passing thorugh its lowest position. What is its speed when it makes an angle of 600 with the vertical? The length of the pendulum is 0.5m Take g=10ms2.
View SolutionBob of the simple pendulum is at rest at its lowest position , Sharp hit imparts a speed of √9gl to the pendium bob. Calculate tension of the thread when it makes an angle 60∘ with the vertical .
View Solution
Knowledge Check
A pendulum bob has a speed of 3ms−1 at its lowest position. The pendulum is 0.5 m long. The speed of the bob, when string makes an angle of 60∘ to the vertical is (take, g=10ms−1)
A2ms−1B12ms−1C1ms−1D2.5ms−1A simple pendulum of length I and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
AmgtanθB−mgsinθCmgsinθD−mgcosθA simple pendulum of length l and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
AmgtanθB−mgsinθCmgsinθD−mgcosθ
A bob of mass 2 kg hangs from a string of length 5 m . It swings from its rest position to one of the sides so that the string makes an angle of 60∘ with the vertical Calculate the gain in potential energy of the bob .
View SolutionThe bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
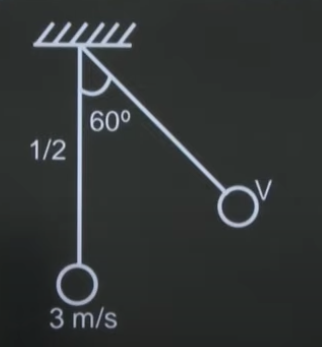
View SolutionA simple pendulum of length 1/2m has initial speed 3m/s when pendulum mass is at lowermost point. What will be the speed pf pendulum mass, when the string of pendulum makes an angle of 600 with vertical.
View SolutionThe bob of a 0.2 m pendulum describes an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is
View SolutionA straight conductor of length 4 m moves at a speed of 10 m/s when the conductor makes an angle of 30∘ with the direction of magnetic induction 0.1 T. then the induced emf is
View Solution
