The bottom of a dip on a road has a radius of curvature R. A richshaw of mass M left a little away from the bottom oscillates about the dip. Deduce an expression for the period of oscillation.
Step by step video & image solution for The bottom of a dip on a road has a radius of curvature R. A richshaw of mass M left a little away from the bottom oscillates about the dip. Deduce an expression for the period of oscillation. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Type D Based on Other Examples of SHM
2 Videos
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Example
202 Videos
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Type B Based on Oscillations
18 Videos
- MOTION IN ONE DIMENSIONBOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice
66 Videos
- Physical worldBOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise
49 Videos
Similar Questions
A small sphere is placed on a concave mirror of radius of curvature 'R' a little away from the centre.When the sphere is released it oscillates.Assuming the oscillation to be simple harmonic its time period is
View SolutionA disc of mass 'm' is suspended at a point R/2 above its centre. Find its period of oscillation.
View Solution
Knowledge Check
In the fig the pulled has a mass M, radius r and the string does not slip over it. The time period of oscillation is
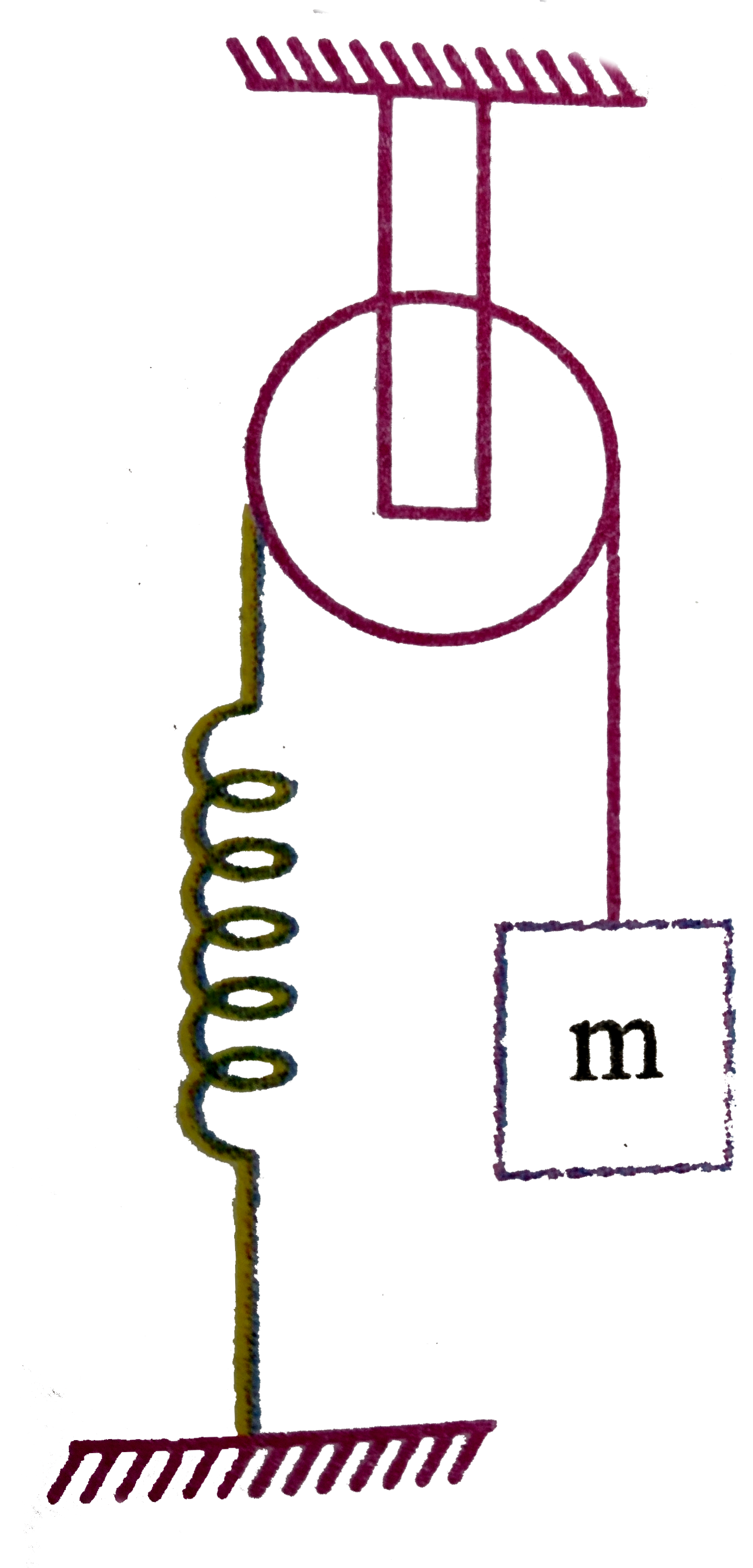 A2π√2m+M2kB2πR√2m+3MR22kC2π√mkD2π√m+Mk
A2π√2m+M2kB2πR√2m+3MR22kC2π√mkD2π√m+MkA disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
A2π√RgB2π√2RgC2π√2π3gD2π√3R2gA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
A2π3√10MKB4π√M3KC4π√MKD2π√M3K
A small block of mass m resting at the bottom of a hemispherical cup of radius R is displaced a little and released. Determine the period of oscillations of the block, assuming the cup to be smooth and fixed rigidly to the table on which it rests. How will period change if the cup is free to move on the table, it is smooth and its mass is M?
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
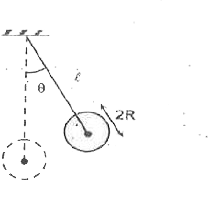
View SolutionA disc is made to oscillate about a horizontal axis passing through mid point of its radius. Determine time period.
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View Solution
A uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring is
View Solution
