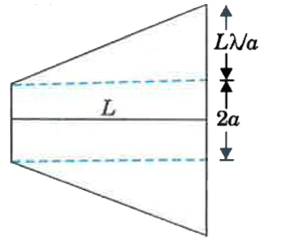
The box of a pinhole camera, of length L, has a hole of radius a. It is assumed that when the hole is illuminated by a parallel beam of light of wavelength λ. The spread of the spot (obtained on the opposite wall of the camera) is the sum of its geometrical spread and the spread due to diffraction. The spot would then have its minimum size (say bmin) when :
A
a=λ2Landbmin=(2λ2L)
B
a=√λLandbmin=(2λ2L)
C
a=√λLandbmin=√4λL
D
a=λ2Landbmin=√4λL
Text Solution
The correct Answer is:C
When a parallel beam of light of wavelength λ illuminates a hole of radius a, it ges diffracted into a beam of angular width :
θ=λa
As the beam travels a distance L, it spreads over a linear width,
x=Lλa
Diameter of the spot , B=2a+2Lλa ....(i)
The minimum size of the spot,
dBda=0 .....(ii)
1−Lλa2=0
⇒a=√λL .....(iii)
Substituting a from equation (iii) in (i)
B=2√λL=2Lλ√λL
Bmin=2√λL+2√λL=4√λL
The radius of the spot, bmin=12(4√λL)=√4λL
|
Topper's Solved these Questions
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - OBJECTIVE TYPE QUESTIONS (JEE (ADVANCED) FOR IIT ENTRANCE)
6 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - OBJECTIVE TYPE QUESTIONS (C. MULTIPLE CHOICE QUESTIONS)
14 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS) -AIPMT/NEET & OTHER STATE BOARDS FOR MEDICAL ENTRANCE
10 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
Knowledge Check
For an aperture of size a illuminated by a parallel beam of light having wavelength 1, the Fresnel distance is:
A=a/λB=a2/λC=a2λD=a/λ2In a pin-hole camera, we usually get
Aerect impressionBinverted impressionCerect imageDinverted imageThe image formed by a pinhole camera is ______.
ArealBinvertedCThe nature of image depends on the shape of pinholeDBoth (a) and (b)
Pinhole camera
View Solution
What determines the size of a pinhole camera image?
View SolutionHow is image in a pinhole camera,possible?
View SolutionA small aperture is illuminated with a parallel beam of λ=628nm. The emergent beam has an anglur divergence of 2∘. The size of the aperture is
View SolutionThe image formed by a pinhole camera is ______.
View Solution
