The breadth of an iron door is 2.4 m. If the minimum torque required to open the door is 50 Nm, what is the minimum force required to open the door?
The correct Answer is:20.8 N
To find the minimum force required to open the door, we can use the formula for torque:
1. Understand the Formula for Torque:
Torque (τ) is defined as the product of the force (F) applied and the perpendicular distance (R) from the pivot point to the line of action of the force. The formula is:
τ=F×R
2. Identify the Given Values:
From the problem, we know:
- Torque (τ) = 50 Nm
- Perpendicular distance (R) = 2.4 m
3. Rearrange the Formula to Solve for Force:
We need to find the force (F), so we rearrange the formula:
F=τR
4. Substitute the Known Values into the Formula:
Now we can substitute the values we have into the rearranged formula:
F=50Nm2.4m
5. Perform the Calculation:
Now, we perform the division:
F=502.4≈20.833N
6. Conclusion:
Therefore, the minimum force required to open the door is approximately:
F≈20.833N
Final Answer:
The minimum force required to open the door is 20.833 Newtons.
---
Torque (τ) is defined as the product of the force (F) applied and the perpendicular distance (R) from the pivot point to the line of action of the force. The formula is:
τ=F×R
From the problem, we know:
- Torque (τ) = 50 Nm
- Perpendicular distance (R) = 2.4 m
We need to find the force (F), so we rearrange the formula:
F=τR
Now we can substitute the values we have into the rearranged formula:
F=50Nm2.4m
Now, we perform the division:
F=502.4≈20.833N
Therefore, the minimum force required to open the door is approximately:
F≈20.833N
The minimum force required to open the door is 20.833 Newtons.
Topper's Solved these Questions
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Picture Study
4 Videos
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section II) Long answer questions
5 Videos
- ENERGYBOOK - ICSECHAPTER - ENERGYEXERCISE - THEME ASSIGNMENT
4 Videos
- HEAT TRANSFER BOOK - ICSECHAPTER - HEAT TRANSFER EXERCISE - Picture Study
2 Videos
Similar Questions
Minimum force F required to move the block
View Solution
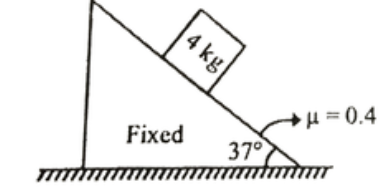
For the given arrangement, find:
(i) Force of friction on the block.
(ii) Acceleration of the block.
(iii) Minimum Force required to prevent the downward sliding of block.
(iv) Minimum Force required to just move the block upwards.
View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA disc is placed on the ground. Friction coefficient is μ. What is the minimum force required to move the disc if it is applied at the topmost point?
View SolutionA nut is opened by a wrench of length 20 cm. If the least force required is 2 N, find the moment of force needed to loosen the nut.
View SolutionA nut is opened by a wrench of length 20 cm. If the least force required is 2 N, find the moment of force needed to loosen the nut.
View SolutionThe minimum force required to move a body up an inclined plane is three times the minimum force required to prevent it from sliding down the plane. If the coefficient of friction between the body and the inclined plane is 12√3, the angle of the inclined plane is
View SolutionThe iron door of a building is 3m broad. It can be opened by applying a force of 100N normally at the middle of the door. Calculate (a) the torque needed to open the door, (b) the least force and its point of application to open the door.
View SolutionA door 1.6 m wide requires a force of 1 N to be applied at the free end to open or close it. The force that is required at a point 0.4 m distant from the hinges for opening or closing the door is
View SolutionIf the lower block is held fixed & force is applied to P, minimum force required to slide P on Q is 12N. Now if Q is free to move on frictionless surface and force is applied to Q then the minimum force F required to slide P on Q is ..........................
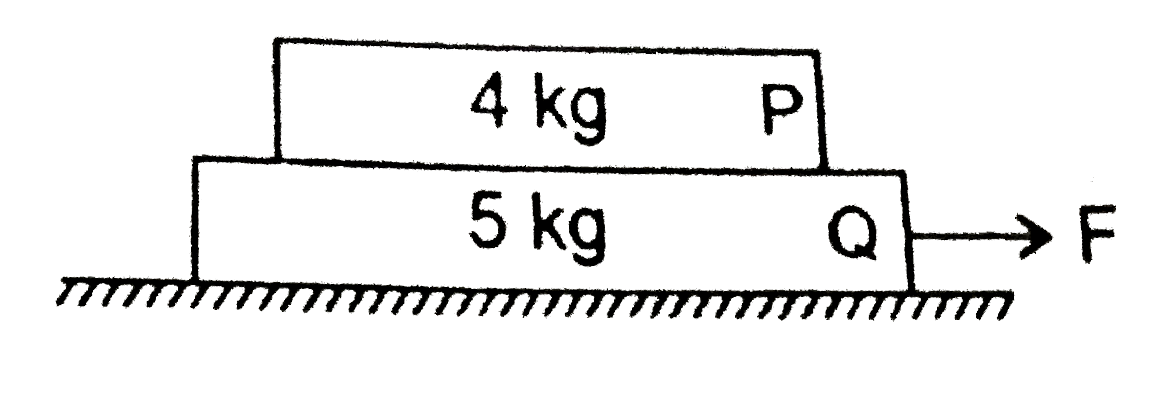
View Solution
