Minimum force F required to move the block
μmg
μmg2
2μmg
μmg4
The correct Answer is:A
To find the minimum force F required to move the block, we can follow these steps:
Step 1: Understand the System
We have a block of mass m resting on a surface with a coefficient of friction μ. The block is connected to a pulley, and we need to determine the minimum force F applied to the pulley to move the block.
Step 2: Draw a Free Body Diagram (FBD)
Draw the free body diagram for the block. The forces acting on the block include:
- The weight of the block mg acting downwards.
- The normal force N acting upwards.
- The frictional force f acting opposite to the direction of motion.
Step 3: Identify the Normal Force
Since there is no vertical motion, the normal force N is equal to the weight of the block:
N=mg
Step 4: Calculate the Frictional Force
The frictional force f can be calculated using the formula:
f=μN
Substituting for N:
f=μmg
Step 5: Analyze the Pulley System
The force F applied to the pulley creates tension T in the string. For the block to start moving, the tension must overcome the frictional force. Therefore, we have:
T=f
Thus,
T=μmg
Step 6: Relate the Force to Tension
In the case of the pulley system, the minimum force F required to move the block is related to the tension in the string. Since the pulley has two segments of the string supporting the block, we have:
F=2T
Substituting for T:
F=2(μmg)
Step 7: Final Expression
Thus, the minimum force F required to move the block is:
F=2μmg
Answer
The minimum force required to move the block is F=2μmg.
---
We have a block of mass m resting on a surface with a coefficient of friction μ. The block is connected to a pulley, and we need to determine the minimum force F applied to the pulley to move the block.
Draw the free body diagram for the block. The forces acting on the block include:
- The weight of the block mg acting downwards.
- The normal force N acting upwards.
- The frictional force f acting opposite to the direction of motion.
Since there is no vertical motion, the normal force N is equal to the weight of the block:
N=mg
The frictional force f can be calculated using the formula:
f=μN
Substituting for N:
f=μmg
The force F applied to the pulley creates tension T in the string. For the block to start moving, the tension must overcome the frictional force. Therefore, we have:
T=f
Thus,
T=μmg
In the case of the pulley system, the minimum force F required to move the block is related to the tension in the string. Since the pulley has two segments of the string supporting the block, we have:
F=2T
Substituting for T:
F=2(μmg)
Thus, the minimum force F required to move the block is:
F=2μmg
The minimum force required to move the block is F=2μmg.
Similar Questions
A block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA block of mass m rests on a rough floor . The coefficient of friction between the block and the floor is μ
a. Two boys apply force P at an angle θ to the horizontal. One of them pushes the block , the other one pulls. Which one would reqire less efferts to cause impending motion of the block?
b. What is the minimum force required to move the block by pulling it ?
c. Shown that the block is pushes at a certain angle θ0 it cannot be moved fro whatever the value of P be
View Solution
Knowledge Check
A cubical box of side L rests on a rough horizontal surface with coefficient of friction p. A horizontal force F is a applied on the block as shown in Fig. 15.4.6. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
Minimum horizontal force (F) required to move the block shown in diagram is__
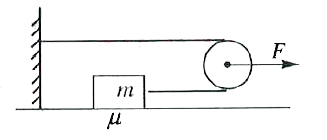
View Solution
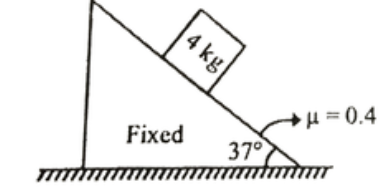
For the given arrangement, find:
(i) Force of friction on the block.
(ii) Acceleration of the block.
(iii) Minimum Force required to prevent the downward sliding of block.
(iv) Minimum Force required to just move the block upwards.
View SolutionIf a pushing force making an angle α with horizontal is applied on a block of mass m placed on horizontal table and angle of friction is β, then minimum magnitude of force required to move the block is
View Solution
Three blocks are connected as shown in the figure. Valculate the minimum force required to move the body with constant velocity. The coefficient of friction at all surfaces is 0.25.
View SolutionA block of mass m=1/3 kg is kept on a rough horizontal plane. Friction coefficient is μ=0.75. The work done by minimum force required to drag to the block along the plane by a distance 5m is :-
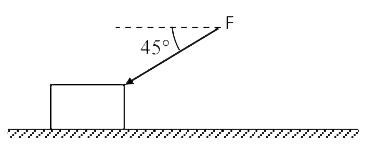
View SolutionWhat minimum force F is required to move this 4 kg block if it acts at an angle of 45∘ as shown ? (μs=0.6)
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View Solution
