The capacitance of a parallel plate capacitor with plate area A and separation s is C. The space between the plates is filled with two wedges of dielectric constants as shown in figure. Find the capacitance of the resultant capacitor.

Let the length of the capacitor plates be l and width b.
Area of each plate, A = lb.
Now consider a small element of the capcitor of width dx at a distance x from the end, as shown in the figure. Its area, dA = bdx.
Capacitance of this small element,
According to the figure,
Putting ,
.

Topper's Solved these Questions
- CAPACITANCE AND CAPACITORBOOK - CHHAYA PUBLICATIONCHAPTER - CAPACITANCE AND CAPACITOREXERCISE - SECTION RELATED QUESTIONS
30 Videos
- CAPACITANCE AND CAPACITORBOOK - CHHAYA PUBLICATIONCHAPTER - CAPACITANCE AND CAPACITOREXERCISE - HIGHER ORDER THINKING SKILL
39 Videos
- ATOMIC NUCLEUSBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMIC NUCLEUSEXERCISE - CBSE SCANNER
14 Videos
- COMMUNICATION STSTEMBOOK - CHHAYA PUBLICATIONCHAPTER - COMMUNICATION STSTEMEXERCISE - CBSE SCANNER
28 Videos
Similar Questions
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View Solution
Knowledge Check
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.

View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

View SolutionYou are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.
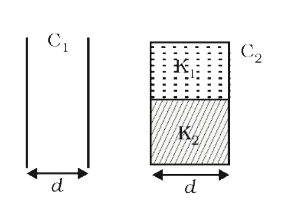
View SolutionYou are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View Solution
