A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

C=C[KK+1]
C'=C[2KK+1]
C'=2CK+1
C'=C[1+K2]
The correct Answer is:B
Answer (2)
1CAB=1(ε0KAd/2)+1(ε0Ad/2)
⇒1CAB=d2ε0A[1K+1]
⇒1CAB=d2ε0A[1+KK]
⇒CAB=2ε0Ad[K1+K]=2C[K1+k]
CAB=C(2K1+K)
Similar Questions
A paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then
 View Solution
View SolutionConsider a parallel plate capacitor. When half of the space between the plates is filled with some dielectric material of dielectric constant K as Shown in Fig. (1) below, the capacitance is C1 . However , if the same dielectric material fills half the space as shown as shown in Fig. (2), the capacitance is C2. Therefore, the ratio C1:C2is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be
A400%B66.6%C33.3%D200%
Consider a parallel plate capacitor of 10μF (micro-farad) with air filled in the gap between the plates. Now one half of the space between the plates is filled with a dielectric of dielectric constant 4, as shown in the figure. The capacity of the capacitor charges to
 View Solution
View SolutionConsider a disconnected plate capacitor of capacity 10μF with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .View Solution
.View SolutionYou are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.
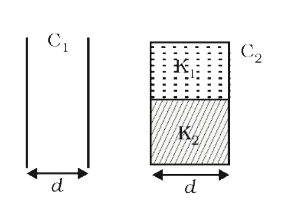 View Solution
View SolutionTwo identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.
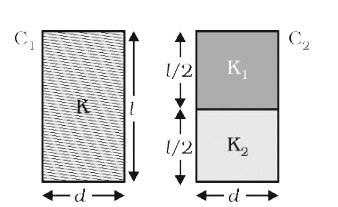 View Solution
View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as where K and a are constants and x is the distance from the left end. Calculate the capacitance.
 View Solution
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.
 View Solution
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 View Solution
View Solution

