The coefficient of friction between a body and the surface of an inclined plane at 45∘ is 0.5. if g=9.8m/s2, the acceleration of the body downwards I m/s2 is
4.9√2
4.9√2
19.6√2
4.9
The correct Answer is:A
To solve the problem, we need to determine the acceleration of a body sliding down an inclined plane at an angle of 45∘ with a coefficient of friction of 0.5. We will use the following steps:
Step 1: Identify the forces acting on the body
The forces acting on the body are:
- The gravitational force acting downwards, mg.
- The component of gravitational force acting parallel to the incline, mgsinθ.
- The component of gravitational force acting perpendicular to the incline, mgcosθ.
- The frictional force acting opposite to the direction of motion, which is given by fk=μN, where N is the normal force.
Step 2: Calculate the components of the gravitational force
For an incline of 45∘:
- mgsin45∘=mg⋅√22
- mgcos45∘=mg⋅√22
Step 3: Calculate the normal force
The normal force N is equal to the component of the gravitational force acting perpendicular to the incline:
N=mgcos45∘=mg⋅√22
Step 4: Calculate the frictional force
The frictional force fk can be calculated using the coefficient of friction:
fk=μN=0.5⋅(mg⋅√22)=0.5mg√22=0.5mg√22=mg√24
Step 5: Set up the equation of motion
The net force Fnet acting on the body in the direction of motion is given by:
Fnet=mgsin45∘−fk
Substituting the values we calculated:
Fnet=mg⋅√22−mg√24
Step 6: Simplify the equation
Factoring out mg:
Fnet=mg(√22−√24)
To combine the terms:
Fnet=mg(2√24−√24)=mg(2√2−√24)=mg(√24)
Step 7: Apply Newton's second law
According to Newton's second law:
Fnet=ma
So we can set up the equation:
mg(√24)=ma
Step 8: Solve for acceleration a
Dividing both sides by m:
g(√24)=a
Substituting g=9.8m/s2:
a=9.8⋅√24
Step 9: Calculate the final value
Calculating the numerical value:
a=9.8√24
To simplify:
a=9.8⋅1.4144≈13.864≈3.465m/s2
Final Answer
The acceleration of the body downwards is approximately 3.465m/s2.
The forces acting on the body are:
- The gravitational force acting downwards, mg.
- The component of gravitational force acting parallel to the incline, mgsinθ.
- The component of gravitational force acting perpendicular to the incline, mgcosθ.
- The frictional force acting opposite to the direction of motion, which is given by fk=μN, where N is the normal force.
For an incline of 45∘:
- mgsin45∘=mg⋅√22
- mgcos45∘=mg⋅√22
The normal force N is equal to the component of the gravitational force acting perpendicular to the incline:
N=mgcos45∘=mg⋅√22
The frictional force fk can be calculated using the coefficient of friction:
fk=μN=0.5⋅(mg⋅√22)=0.5mg√22=0.5mg√22=mg√24
The net force Fnet acting on the body in the direction of motion is given by:
Fnet=mgsin45∘−fk
Substituting the values we calculated:
Fnet=mg⋅√22−mg√24
Factoring out mg:
Fnet=mg(√22−√24)
To combine the terms:
Fnet=mg(2√24−√24)=mg(2√2−√24)=mg(√24)
According to Newton's second law:
Fnet=ma
So we can set up the equation:
mg(√24)=ma
Dividing both sides by m:
g(√24)=a
Substituting g=9.8m/s2:
a=9.8⋅√24
Calculating the numerical value:
a=9.8√24
To simplify:
a=9.8⋅1.4144≈13.864≈3.465m/s2
The acceleration of the body downwards is approximately 3.465m/s2.
Topper's Solved these Questions
Similar Questions
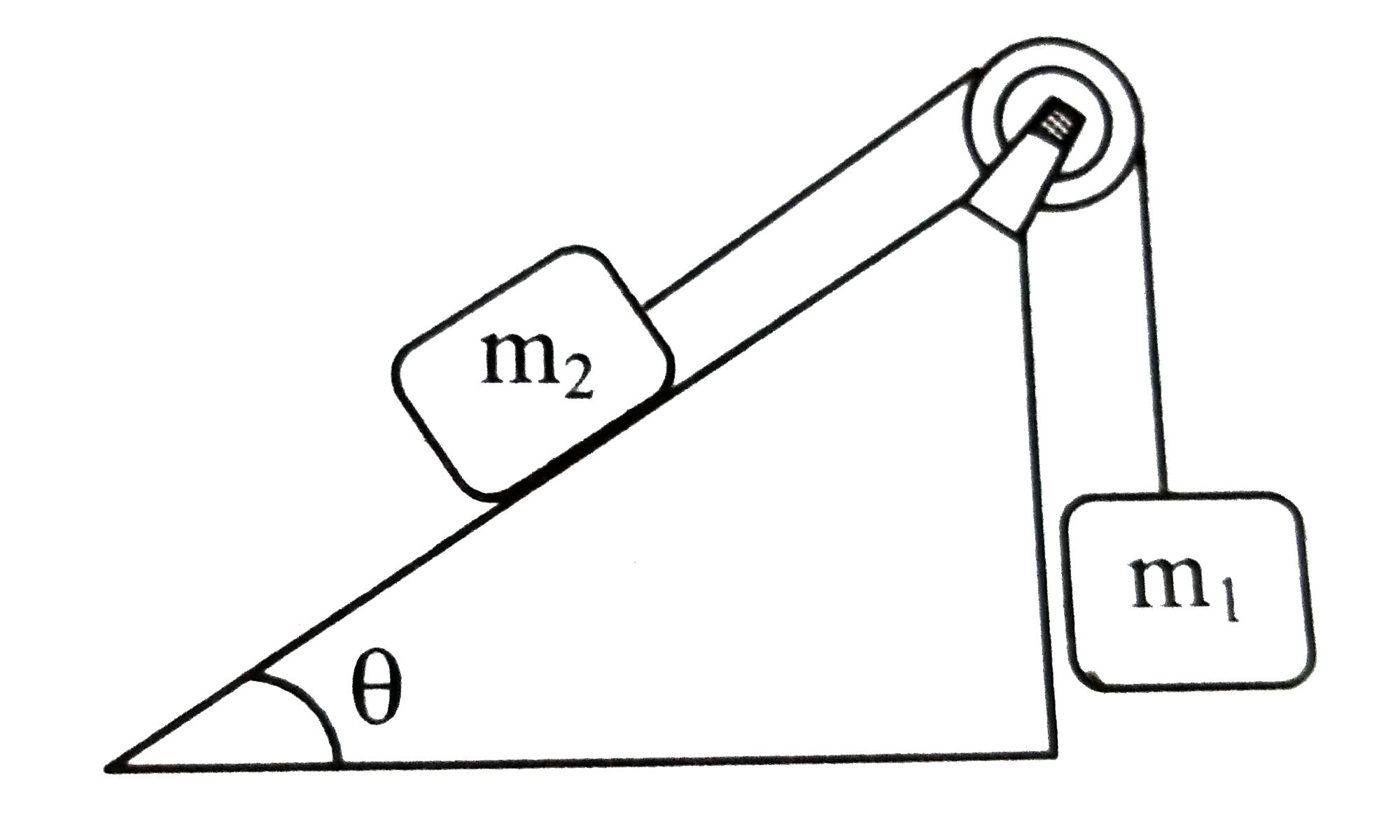
The coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View Solution
Knowledge Check
The angle of inclination of an inclined plane is 60∘. Coefficient of friction between 10kg body on it and its surface is 0.2, g=10ms−2. The acceleration of the body down the plane in ms−2 is
A5.667B6.66C7.66DZeroThe angle of inclination of an inclined plane is 60∘. Coefficient of friction between 10kg body on it and its surface is 0.2,g=10ms−2. The acceleration of the body down the plane in ms−2 is .
A5.667B6.66C7.66DZeroThe angle of inclination of an inclined plane is 60∘. Coefficient of friction between 10kg body on it and its surface is 0.2,g=10ms−2. The acceleration of the body down the plane in ms−2 is
In the above problem the minimum, force required to pull the body up the inclined plane .A66.6NB86.6NC96.6ND76.6N
The angle of inclination of an inclined plane is 60∘. Coefficient of friction between 10kg body on it and its surface is 0.2,g=10ms−2. The acceleration of the body down the plane in ms−2 is .
In the above problem the frictional force on the body is .
View SolutionThe angle of inclination of an inclined plane is 60∘. Coefficient of friction between 10kg body on it and its surface is 0.2,g=10ms−2. The acceleration of the body down the plane in ms−2 is .
In the above problem the minimum force on the body is .
View SolutionA body is kept on a horizontal disc of radius 2 m at a distance of 1 m from the centre . The coefficient of friction between the body and the surface of disc is 0.4. The speed of rotation of the disc at which the body starts slipping is (g=10m/s2)
View SolutionA block is lying on an inclined plane which makes 60∘ with the horizontal. If coefficient of friction between block and plane is 0.25 and g=10m/s2, , then acceleration of the block when it moves along the plane will be
View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :

View Solution