The coefficient of friction between the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is (Take g=10ms−2)
√15ms−1
√3ms−1
√30ms−1
√10ms−1
The correct Answer is:B
To find the maximum speed with which a cyclist can take a circular turn without skidding, we can use the formula derived from the concepts of circular motion and friction.
1. Identify the Given Values:
- Coefficient of friction (μ) = 0.1
- Radius of the circular turn (r) = 3 m
- Acceleration due to gravity (g) = 10 m/s²
2. Use the Formula for Maximum Speed:
The formula to calculate the maximum speed (V_max) at which a cyclist can take a turn without skidding is:
Vmax=√μ⋅r⋅g
3. Substitute the Values into the Formula:
Now, substitute the values of μ, r, and g into the formula:
Vmax=√0.1⋅3⋅10
4. Calculate the Value Inside the Square Root:
First, calculate the product:
0.1⋅3⋅10=3
5. Take the Square Root:
Now, take the square root of the result:
Vmax=√3 m/s
6. Final Result:
Therefore, the maximum speed with which the cyclist can take the turn without skidding is:
Vmax=√3 m/s
Conclusion:
The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is √3 m/s.
---
- Coefficient of friction (μ) = 0.1
- Radius of the circular turn (r) = 3 m
- Acceleration due to gravity (g) = 10 m/s²
The formula to calculate the maximum speed (V_max) at which a cyclist can take a turn without skidding is:
Vmax=√μ⋅r⋅g
Now, substitute the values of μ, r, and g into the formula:
Vmax=√0.1⋅3⋅10
First, calculate the product:
0.1⋅3⋅10=3
Now, take the square root of the result:
Vmax=√3 m/s
Therefore, the maximum speed with which the cyclist can take the turn without skidding is:
Vmax=√3 m/s
The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is √3 m/s.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - HOTS
8 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exemplar Problems
9 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tyre and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionA car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
View Solution
Knowledge Check
The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g=10ms−2)
A2ms−2B4ms−2C6ms−2D8ms−2
The coefficient of friction between the tyres and road is 0.4. The minimum distance covered before attaining a speed of 8ms−1 starting from rest is nearly ( take g=10ms−2)
View SolutionA car is driven round a curved path of radius 18 m without the danger of skidding. The coefficient of friction between the tyres of the car and the surface of the curved path is 0.2. What is the maximum speed in kmph of the car for safe driving ? [g = 10ms−1]
View SolutionThe maximum speed with which a vehicle can take safely circular turn on a horizontal flat rough road is (where symbols have their usual meanings)
View SolutionWhat is the maximum speed with which a cylist can turn around curved path of radius 10.0 m, if the coefficient of friction between the tyre and the road is 0.5 ? If the cyclist wants to avoid overturning by what angle the cyclist must lean from the vertical ?
View SolutionConsider, a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between the tyre and the road is 0.5, the shortest distance in which the car can be stopped is (Take g=10/s2)
View SolutionAn automobile enters a turn of radius R. If the road is banked at an angle of 45∘ and the coefficient of friction is 1, the minimum and maximum speed with which the automobile can negotiate the turn without skidding is :
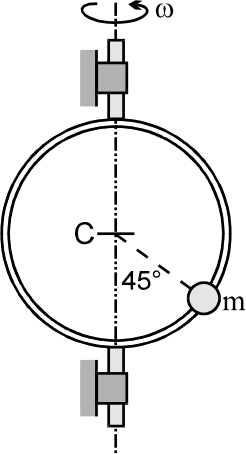
View SolutionA small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
View Solution