The conduction current is the same as displacement current when the source is
ac only
dc only
either ac or dc
neither dc nor ac
The correct Answer is:C
To determine when the conduction current is the same as the displacement current, we can analyze the situation using the concepts of capacitors and the nature of the currents involved.
1. Understanding Conduction and Displacement Current:
- Conduction current is the actual flow of charge through a conductor.
- Displacement current is a concept introduced by Maxwell to account for changing electric fields in situations where there is no actual charge flow, such as in a capacitor.
2. Capacitor Behavior:
- In a capacitor, the relationship between charge (Q), capacitance (C), and voltage (V) is given by the equation:
Q=C⋅V
- The current (I) flowing through the capacitor can be expressed as:
I=dQdt
- By substituting the expression for Q, we get:
I=C⋅dVdt
3. Analyzing Current with Constant Voltage:
- If the voltage (V) across the capacitor is constant, then dVdt=0. This implies:
I=C⋅0=0
- Therefore, when the voltage is constant (like in a DC source), the conduction current is zero.
4. Analyzing Current with Time-Varying Voltage:
- In contrast, if the voltage across the capacitor is time-varying (as in an AC source), then dVdt is not zero, and thus:
I=C⋅dVdt≠0
- In this case, the displacement current, which is defined as:
Id=ϵ0⋅dEdt
where E is the electric field, also contributes and is non-zero.
5. Conclusion:
- The conduction current is equal to the displacement current when the source is an AC voltage source. This is because both currents are active and contribute to the total current in the circuit.
Final Answer:
The conduction current is the same as the displacement current when the source is an AC voltage source.
- Conduction current is the actual flow of charge through a conductor.
- Displacement current is a concept introduced by Maxwell to account for changing electric fields in situations where there is no actual charge flow, such as in a capacitor.
- In a capacitor, the relationship between charge (Q), capacitance (C), and voltage (V) is given by the equation:
Q=C⋅V
- The current (I) flowing through the capacitor can be expressed as:
I=dQdt
- By substituting the expression for Q, we get:
I=C⋅dVdt
- If the voltage (V) across the capacitor is constant, then dVdt=0. This implies:
I=C⋅0=0
- Therefore, when the voltage is constant (like in a DC source), the conduction current is zero.
- In contrast, if the voltage across the capacitor is time-varying (as in an AC source), then dVdt is not zero, and thus:
I=C⋅dVdt≠0
- In this case, the displacement current, which is defined as:
Id=ϵ0⋅dEdt
where E is the electric field, also contributes and is non-zero.
- The conduction current is equal to the displacement current when the source is an AC voltage source. This is because both currents are active and contribute to the total current in the circuit.
The conduction current is the same as the displacement current when the source is an AC voltage source.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - HOTS
8 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - NCERT EXEMPLAR PROBLEMS
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT Exemplar
6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
In the question 3, the ratio of conduction current and the displacement current is
A(aπλ)2B(aπλ)C(λaπ)2D(λ2π)A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.A2πλ2I0ln(as)sin(2πυt)ˆkB1λ2I0ln(as)sin(2πυt)ˆkCπλ2I0ln(as)sin(2πυt)ˆkDZero
(A) : In Ampere Maxwell law, displacement current has same physical effect as conduction current. (R) : The units and dimensions of displacement current and conduction current are same.
View Solution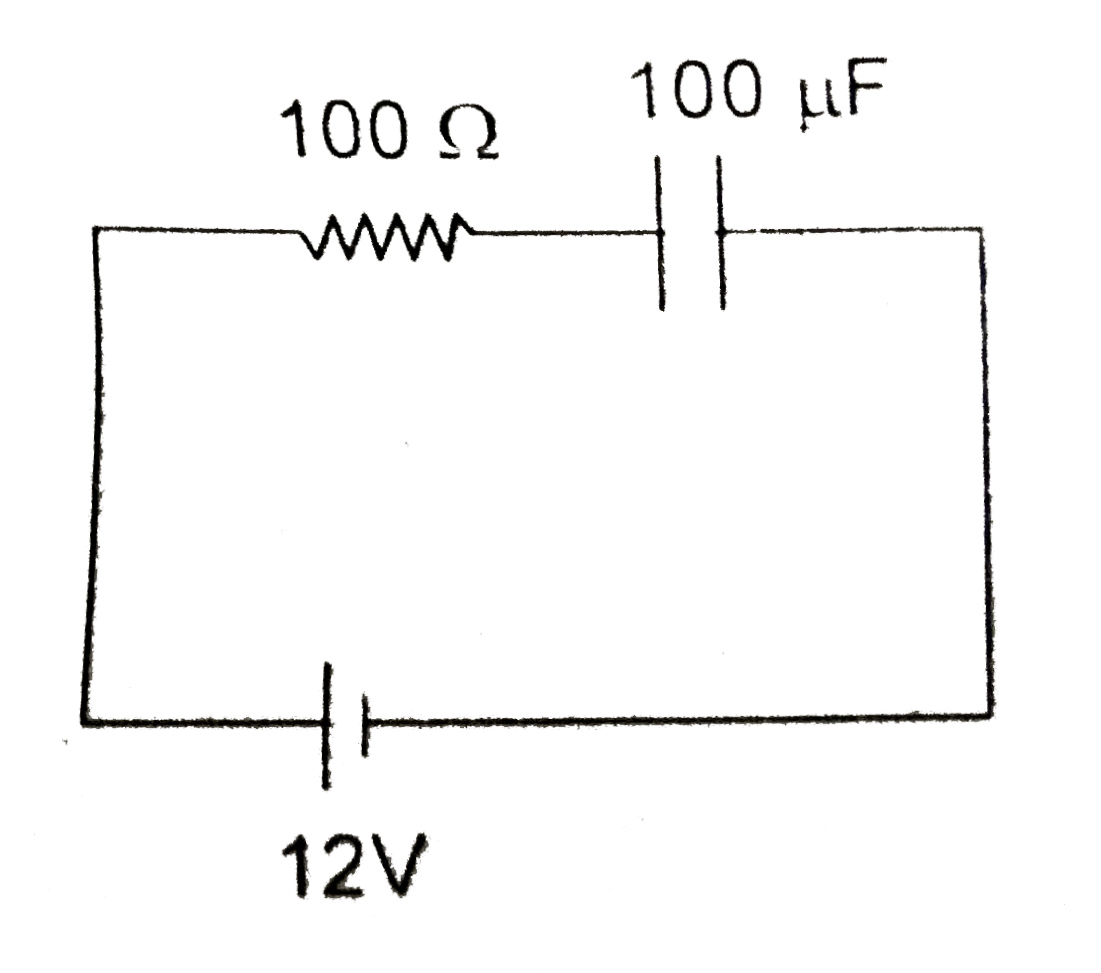
The value of displacement current at t=1 time constant is
View SolutionA parallel plate capacitor 20 μF is being charged by a voltage source whose potential is changing at the rate of 3 V/s. The conduction current through the connecting wires, and the displacement current through the plates of the capacitor, would be, respectively:
View Solution(A ): When a capacitor is getting charged the conduction current in the connecting wires at any instant is equal to the displacement current in between the capacitor plates. (R) : Conduction current is always greater than the displacement current.
View SolutionA capacitor, made of two parallel plates each of plate area A and separation d, is being charged by an external ac socurce. Show that the displacement current inside the same as the current charging the capacitor.
View SolutionA capacitor, made of two parallel plates each of plate area A and separation d, is being charged by an external ac socurce. Show that the displacement current inside the same as the current charging the capacitor.
View Solution
