(A) : In Ampere Maxwell law, displacement current has same physical effect as conduction current. (R) : The units and dimensions of displacement current and conduction current are same.
Both 'A' and 'R' are true and 'R' is the correct explanation of 'A'.
Both 'A' and ’R' are true and 'R' is not the correct explanation of 'A
A' is true and 'R' is false
'A' is false and R' is true
The correct Answer is:B
To solve the question, we need to analyze both the assertion (A) and the reason (R) provided:
1. Understanding the Assertion (A):
- The assertion states that "In Ampere-Maxwell law, displacement current has the same physical effect as conduction current."
- In the context of Ampere-Maxwell law, both conduction current (I_c) and displacement current (I_d) contribute to the total current in a circuit. The law can be expressed as:
∮B⋅dL=μ0(Ic+Id)
- Here, Ic is the conduction current, which is the flow of charge due to electric field in a conductor, while Id is the displacement current, which arises due to a changing electric field in regions where there is no conduction current (like in a capacitor).
2. Understanding the Reason (R):
- The reason states that "The units and dimensions of displacement current and conduction current are the same."
- The displacement current Id is defined as:
Id=ϵ0dΦEdt
- Here, ϵ0 is the permittivity of free space and ΦE is the electric flux. The units of displacement current Id are the same as that of conduction current Ic, which is Amperes (A).
3. Conclusion:
- Both the assertion and the reason are true statements. However, the reason does not provide a correct explanation for the assertion. The assertion is about the physical effect of both types of current, while the reason discusses their units and dimensions.
Final Answer:
- Both (A) and (R) are true, but (R) is not the correct explanation of (A).
- The assertion states that "In Ampere-Maxwell law, displacement current has the same physical effect as conduction current."
- In the context of Ampere-Maxwell law, both conduction current (I_c) and displacement current (I_d) contribute to the total current in a circuit. The law can be expressed as:
∮B⋅dL=μ0(Ic+Id)
- Here, Ic is the conduction current, which is the flow of charge due to electric field in a conductor, while Id is the displacement current, which arises due to a changing electric field in regions where there is no conduction current (like in a capacitor).
- The reason states that "The units and dimensions of displacement current and conduction current are the same."
- The displacement current Id is defined as:
Id=ϵ0dΦEdt
- Here, ϵ0 is the permittivity of free space and ΦE is the electric flux. The units of displacement current Id are the same as that of conduction current Ic, which is Amperes (A).
- Both the assertion and the reason are true statements. However, the reason does not provide a correct explanation for the assertion. The assertion is about the physical effect of both types of current, while the reason discusses their units and dimensions.
- Both (A) and (R) are true, but (R) is not the correct explanation of (A).
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -IA
47 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise
11 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
Similar Questions
Knowledge Check
The conduction current is the same as displacement current when the source is
Aac onlyBdc onlyCeither ac or dcDneither dc nor acIn the question 3, the ratio of conduction current and the displacement current is
A(aπλ)2B(aπλ)C(λaπ)2D(λ2π)A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.A2πλ2I0ln(as)sin(2πυt)ˆkB1λ2I0ln(as)sin(2πυt)ˆkCπλ2I0ln(as)sin(2πυt)ˆkDZero
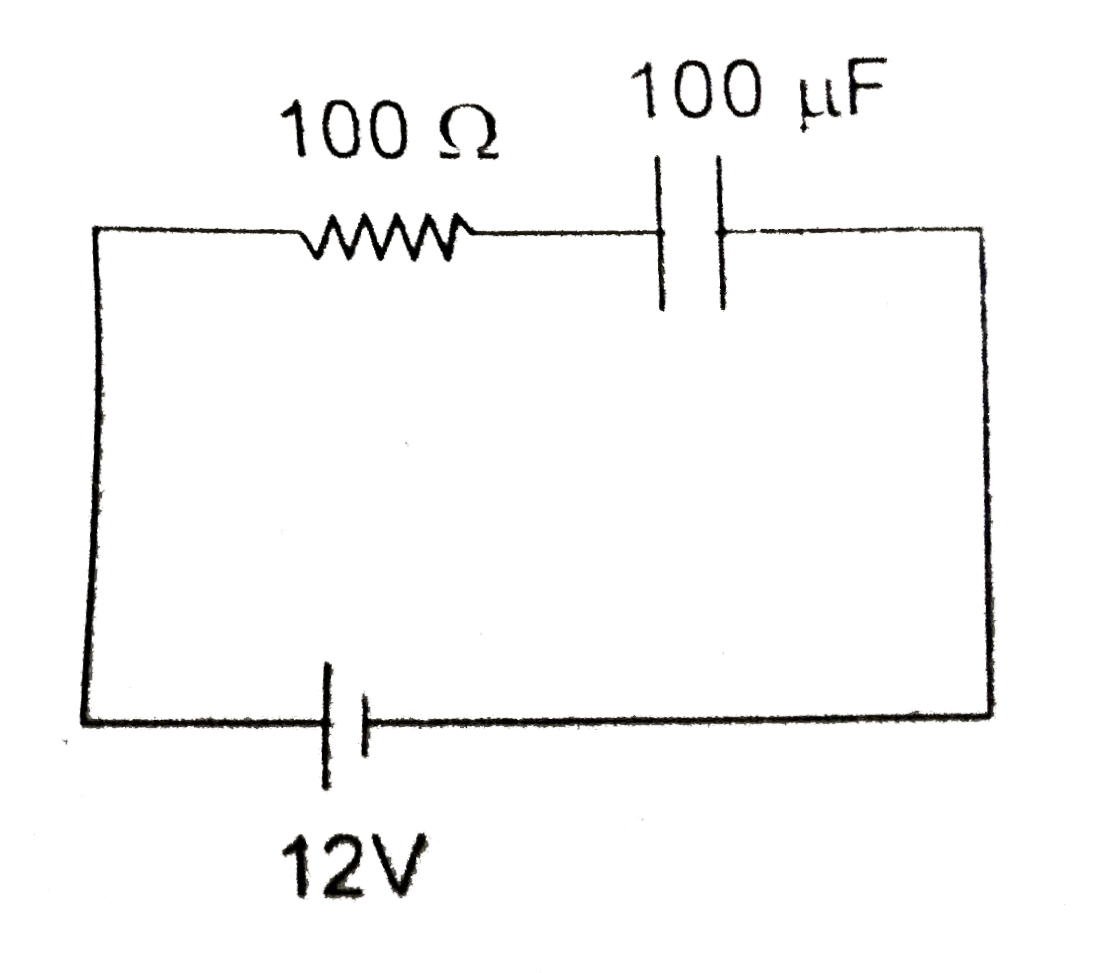
The value of displacement current at t=1 time constant is
View SolutionShow that displacement current is equal to conduction during charging of a capacitor.
View SolutionThe charging current for a capacitor is 1 A, then the displacement current is
View SolutionThe magnetic dipole moment of a current carrying conducting loop depends on
View SolutionWhen a capacitor is charged then
lc= conduction current ld = displacembet current)
View Solution
