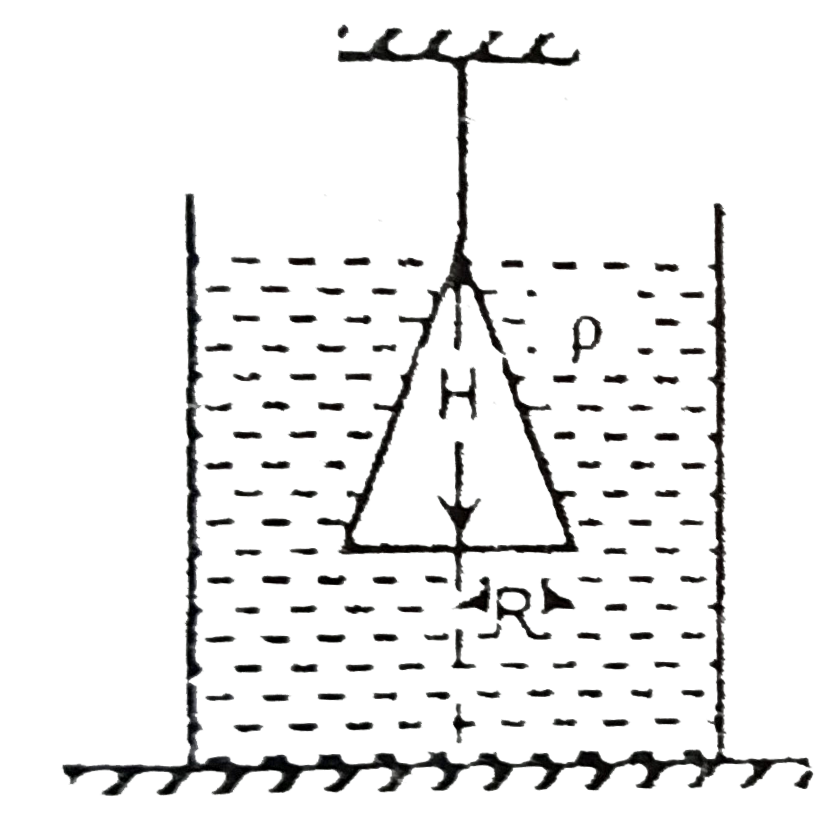
The cone of radius $R$ and height $H$ is hanging inside a liquid of density by means of a string a shwon in the figure.

A

Net force on the cone by the liquid is equal to buoyancy force on the cone.

B

Force on the bottom surfae of the cone is more than buoyancy force on the cone.

C

Net force on the slant surface of the cone is more than buoyancy force on the cone.

D

Net force on the slant surface of the cone is less than buoyancy force on the cone.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

$B = F_{B} - F_{S}$ , where $F_{S}$ is the net vertical downward force on the slant surface and $F_{B}$ is net force on the bottom surface.

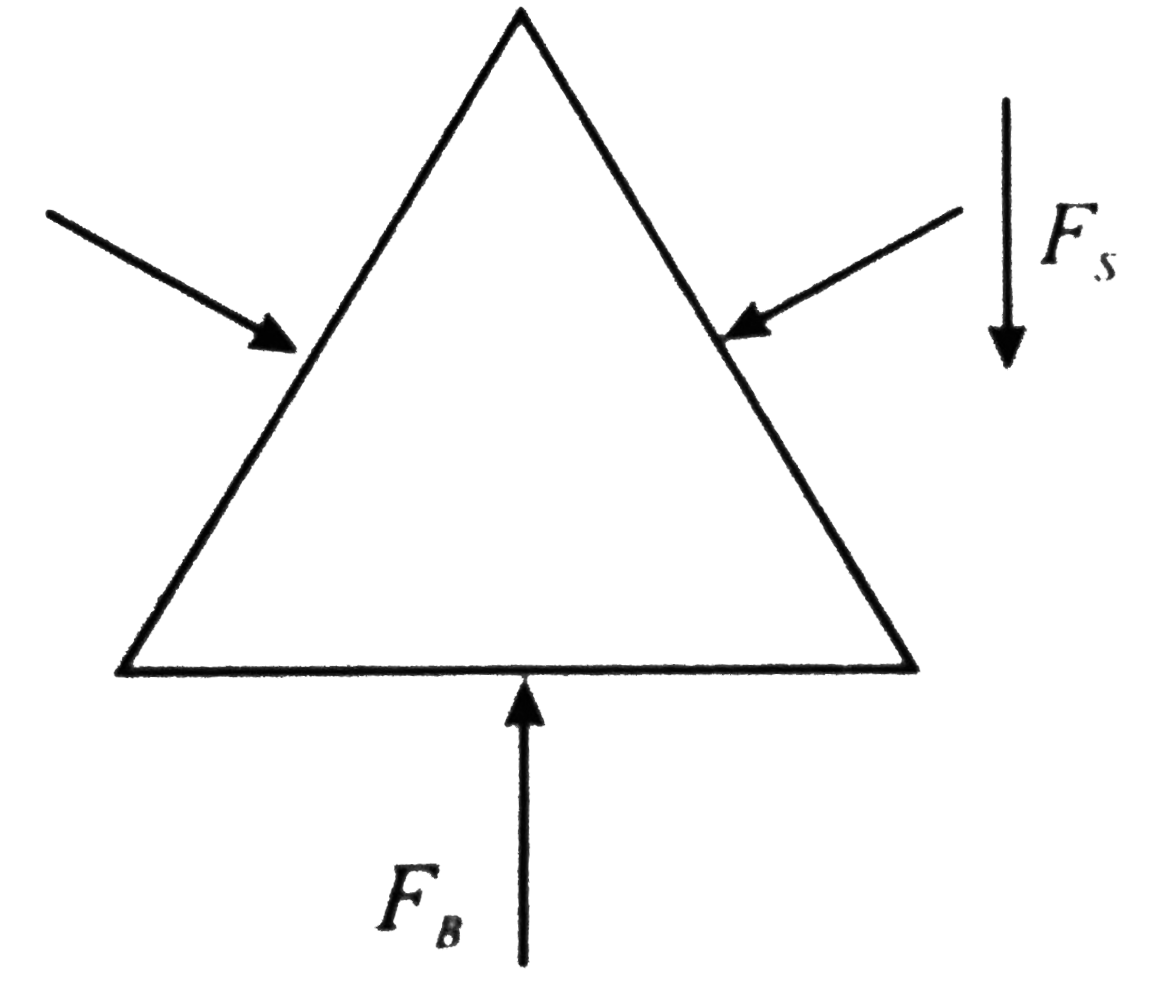
$B = V ρ g = \frac{1}{3} π R^{2} ρ g, F_{B} = ρ g H π R^{2}$
Now $F_{s} = F_{b} - B$
$\Rightarrow F_{S} = ρ g H π R^{2} - \frac{H ρ g π R^{2}}{3} = \frac{2}{3} ρ g H π R^{2}$
Clearly $F_{B} > B, F_{S} > B$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cone of radius $R$ and height $H$ , is hanging inside a liquid of density $ρ$ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is

A $ρ π g H R^{2}$
B $π ρ g H R^{2}$
C $\frac{4}{3} π ρ g H R^{2}$
D $\frac{2}{3} π ρ g H R^{2}$
Question 2 - Select One

A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)
A $π r^{2} d g (H - \frac{r}{3})$
B $2 π r^{2} d g (H - \frac{2 r}{3})$
C $π r^{2} d g (2 H - \frac{r}{3})$
D $π r^{2} d g (2 H - \frac{2 r}{3})$
Question 3 - Select One
A sphere of radius R and density $ρ_{1}$ is dropped in a liquid of density $σ$ . Its terminal velocity is $v_{1}$ . If another sphere of radius $R$ and density $ρ_{2}$ is dropped in the same liquid, its terminal velocity will be:
A $(\frac{ρ_{2} - σ}{ρ_{1} - σ}) v_{1}$
B $(\frac{ρ_{1} - σ}{ρ_{1} - σ}) v_{1}$
C $(\frac{ρ_{1}}{ρ_{2}}) v_{1}$
D $(\frac{ρ_{2}}{ρ_{1}}) v_{1}$

CENGAGE PHYSICS-MISCELLANEOUS VOLUME 2-MCQ_TYPE

Home
Ask Doubt
Profile