From a uniform solid cone of base radius R and height H, a symmetric cone of the base radius R2 is removed as shown. Then the centre of mass is shifted by H/n. Find the value of of n.
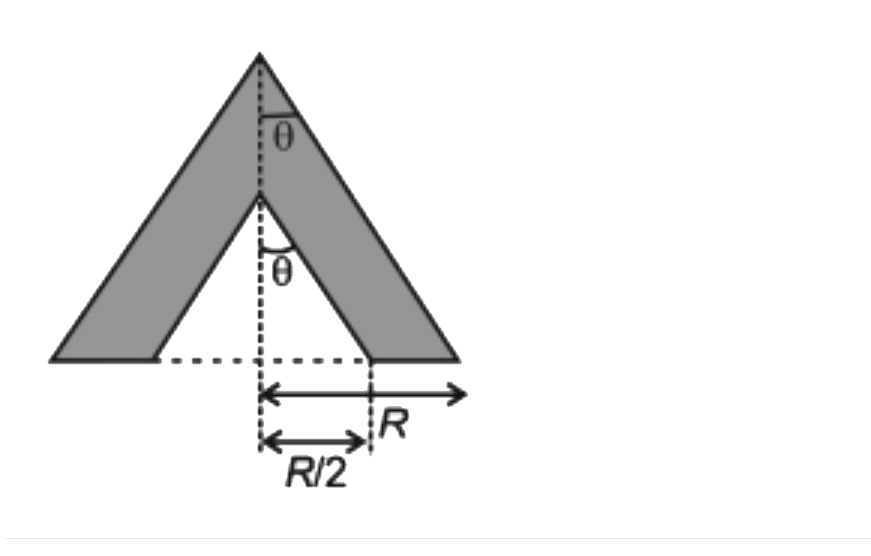
The correct Answer is:56
Step by step video, text & image solution for From a uniform solid cone of base radius R and height H, a symmetric cone of the base radius (R)/(2) is removed as shown. Then the centre of mass is shifted by H/n. Find the value of of n. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
From a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View SolutionA frustum of a uniform solid cone has base radius R and height H as shown. Radius of top surface is R2. If height of centre of mass of frustum is 11H4n from base then n will be.

View Solution
Knowledge Check
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
 A1.5RB√3RC3RD2√3R
A1.5RB√3RC3RD2√3RA solid metallic cylinder of base radius 3 cm and height 5 cm is melted to make n solid cones of height 1 cm and base radius 1 mm. The value of n is
A450B1350C4500D13500From a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
A240π cu. cmB5280 cu. cmC620π cu. cmD360π cu. cm
Find the centre of mass of a uniform solid cone.
View SolutionFrom a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
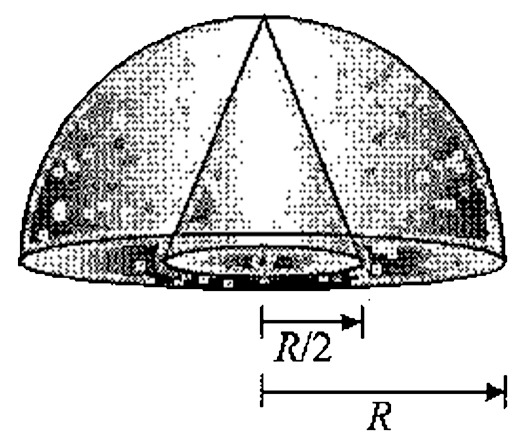
View SolutionThe curved surface area of a cone of base radius r and height h is_______.
View SolutionA uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown in the figure. The centre of mass of the.composite solid lies at the centre of base of the cone. The height of the cone is √xR. Find x.
'(##CEN_KSR_PHY_JEE_C08_E01_017_Q10##)'
View SolutionA solid metallic cylinder of base 3 cm and height 5 cm is melted to make n solid cones of height 1 mm and base radius 1 mm. Then, is the value of n is
View Solution