The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
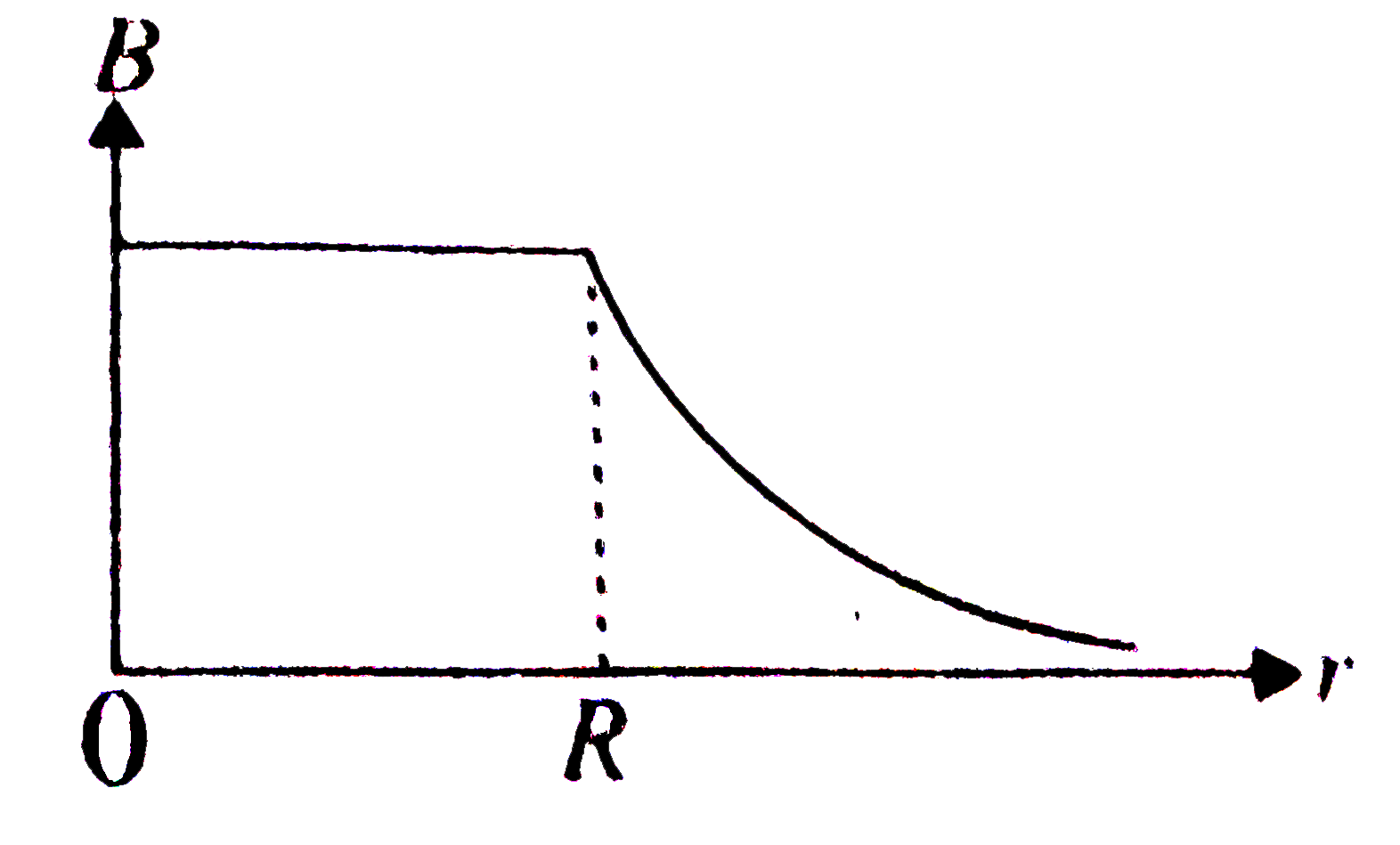
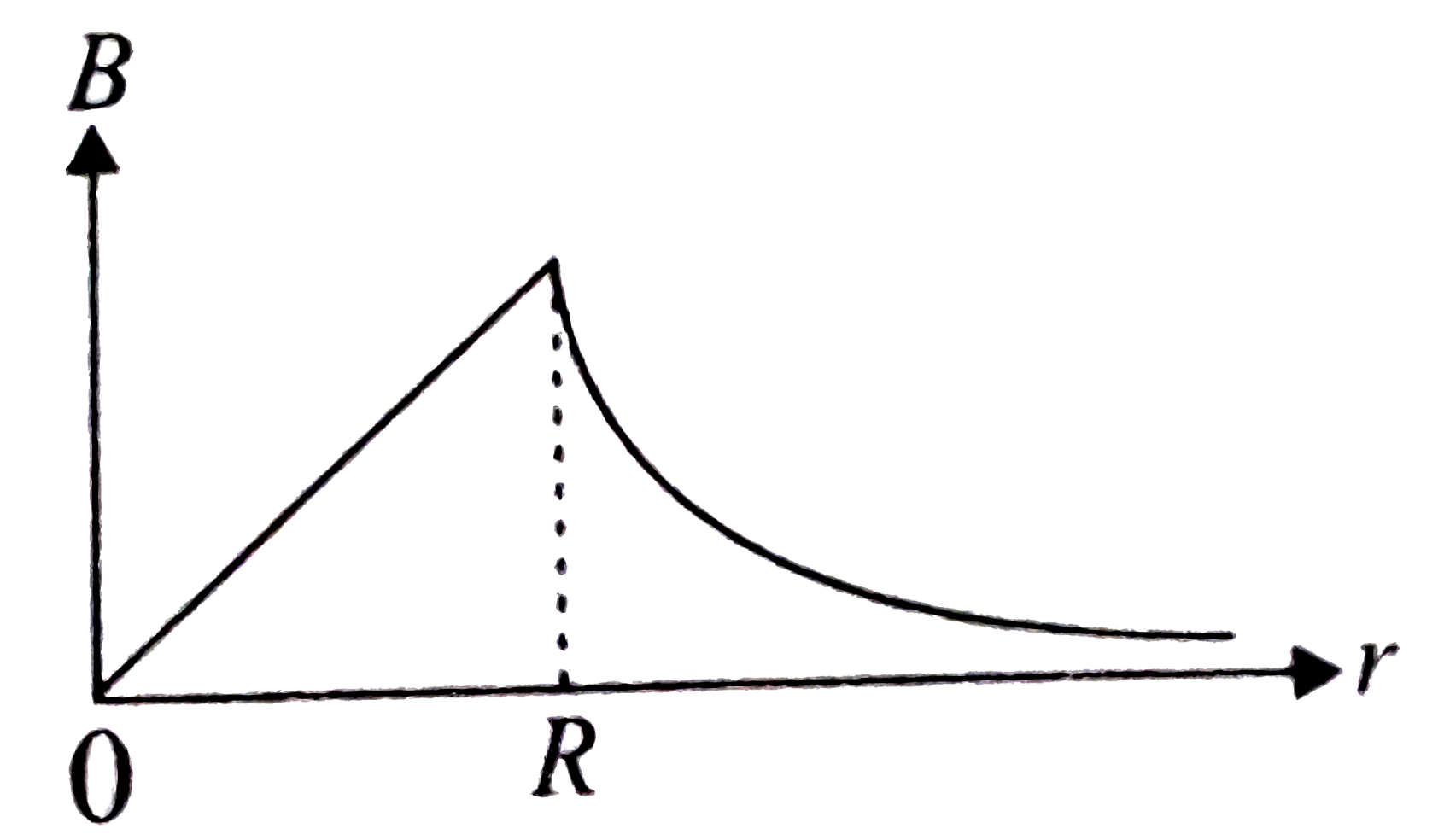
The correct Answer is:B
To solve the problem of plotting the magnitude of the magnetic field →B versus the distance r from the center of a wire with radius R carrying a current I, we can follow these steps:
Step 1: Understanding the Magnetic Field Inside the Wire
When we are inside the wire (i.e., r<R), the magnetic field B can be determined using Ampere's Law. For a uniformly current-carrying wire, the magnetic field inside the wire increases linearly with the distance from the center. The formula for the magnetic field inside the wire is given by:
B=μ0Ir2πR2
where μ0 is the permeability of free space, I is the current flowing through the wire, r is the distance from the center, and R is the radius of the wire.
Step 2: Understanding the Magnetic Field at the Surface of the Wire
At the surface of the wire (i.e., when r=R), the magnetic field can be calculated using the formula:
B=μ0I2πR
This represents the maximum value of the magnetic field inside the wire.
Step 3: Understanding the Magnetic Field Outside the Wire
When we are outside the wire (i.e., r>R), the magnetic field decreases with the distance from the center of the wire. The formula for the magnetic field outside the wire is:
B=μ0I2πr
This shows that the magnetic field is inversely proportional to the distance from the center of the wire.
Step 4: Plotting the Magnetic Field
Now, we can summarize the behavior of the magnetic field B as follows:
- For r<R: B increases linearly with r.
- For r=R: B reaches a maximum value of μ0I2πR.
- For r>R: B decreases inversely with r.
Step 5: Drawing the Graph
1. Start the graph at the origin (0,0).
2. As r increases from 0 to R, draw a straight line that rises linearly.
3. At r=R, mark the maximum value of B.
4. After r=R, draw a curve that decreases towards the x-axis, approaching zero but never touching it.
Conclusion
The correct plot of the magnitude of the magnetic field B versus distance r from the center of the wire is characterized by an initial linear increase (for r<R), reaching a maximum at r=R, and then a decrease (for r>R) that follows an inverse relationship.
When we are inside the wire (i.e., r<R), the magnetic field B can be determined using Ampere's Law. For a uniformly current-carrying wire, the magnetic field inside the wire increases linearly with the distance from the center. The formula for the magnetic field inside the wire is given by:
At the surface of the wire (i.e., when r=R), the magnetic field can be calculated using the formula:
When we are outside the wire (i.e., r>R), the magnetic field decreases with the distance from the center of the wire. The formula for the magnetic field outside the wire is:
Now, we can summarize the behavior of the magnetic field B as follows:
- For r<R: B increases linearly with r.
- For r=R: B reaches a maximum value of μ0I2πR.
- For r>R: B decreases inversely with r.
1. Start the graph at the origin (0,0).
2. As r increases from 0 to R, draw a straight line that rises linearly.
3. At r=R, mark the maximum value of B.
4. After r=R, draw a curve that decreases towards the x-axis, approaching zero but never touching it.
The correct plot of the magnitude of the magnetic field B versus distance r from the center of the wire is characterized by an initial linear increase (for r<R), reaching a maximum at r=R, and then a decrease (for r>R) that follows an inverse relationship.
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - The Solenoid And The Toroid5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Force Between The Parallel Currents, The Ampere6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Magnetic Field On The Axis Of A Circular Current Loop8videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTIPSCHAPTER - MAGNETISM AND MATTER EXERCISE - Assertion And Reason15videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
There are two separate long cylindrical wires having uniform current density. The radius of one of the wires is twice that of the other. The fig. shows the plot of magni- tude of magnetic field intensity versus radial distance (r) from their axis. The curved parts of the two graphs are overlapping. Find the ratio B1:B2.
 View Solution
View SolutionThe volume charge density of a sphere carrying charge Q and of radius R is proportional to the square of the distance from the centre. The ratio of the magnitude of the electric field at a distance 2R from the centre to that at a distance of R2 from the centre is
View Solution
Knowledge Check
- Question 1 - Select One
A cylinderical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
A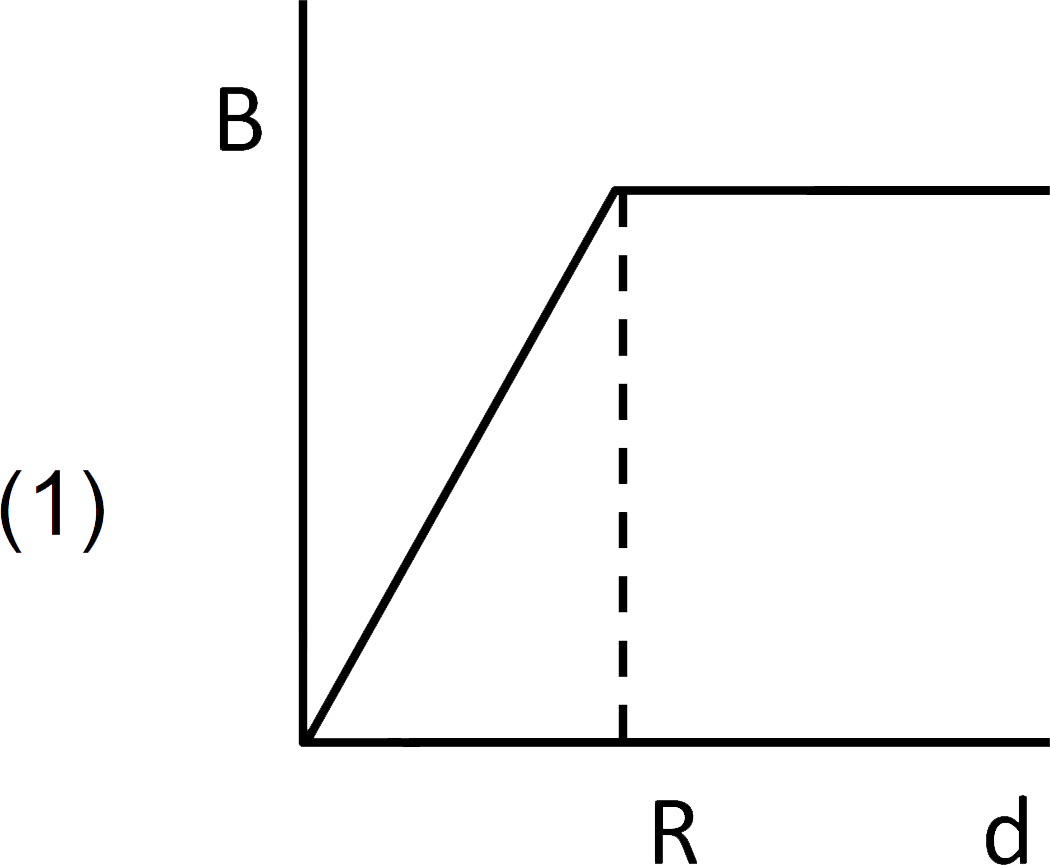 B
B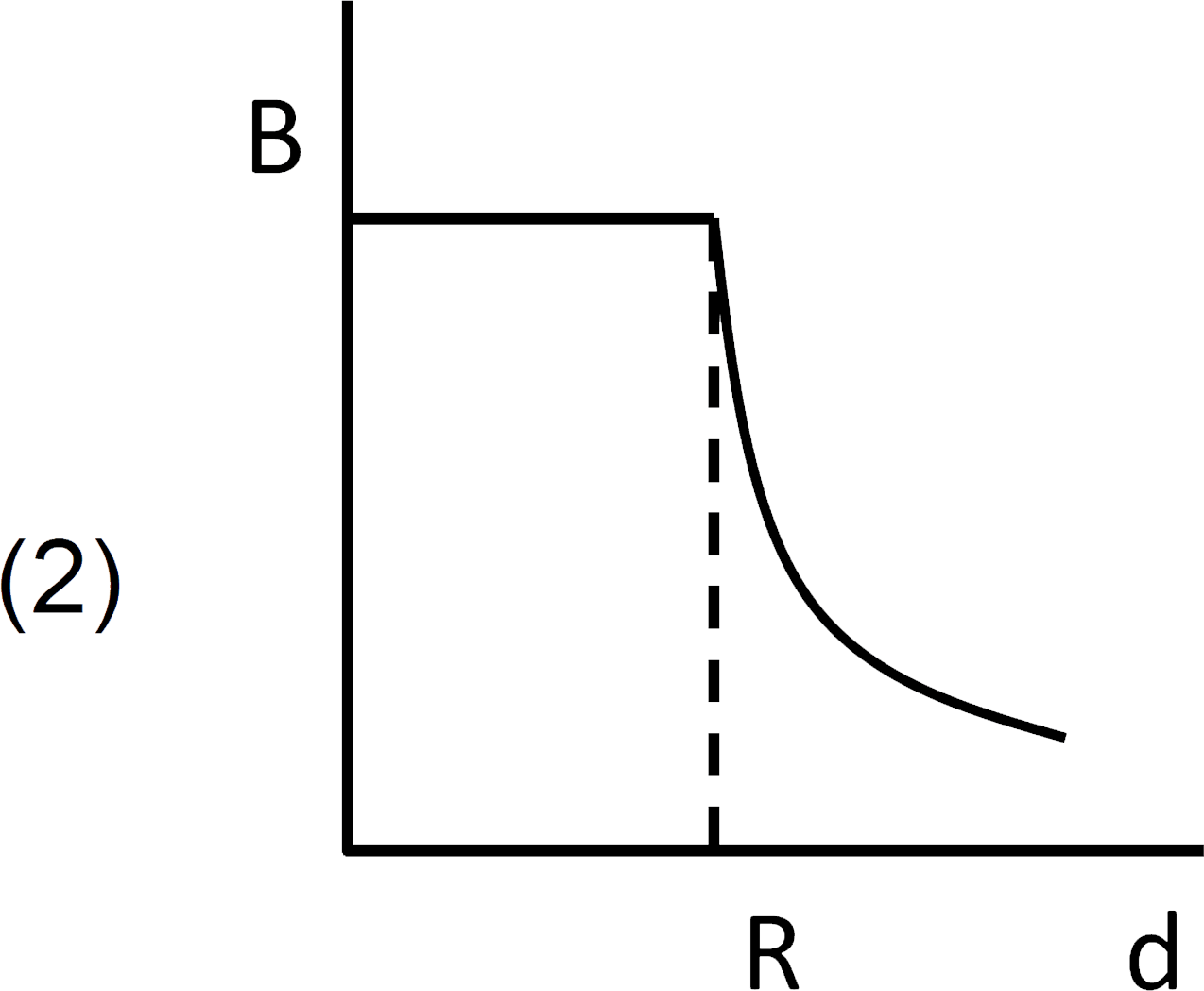 C
C D
D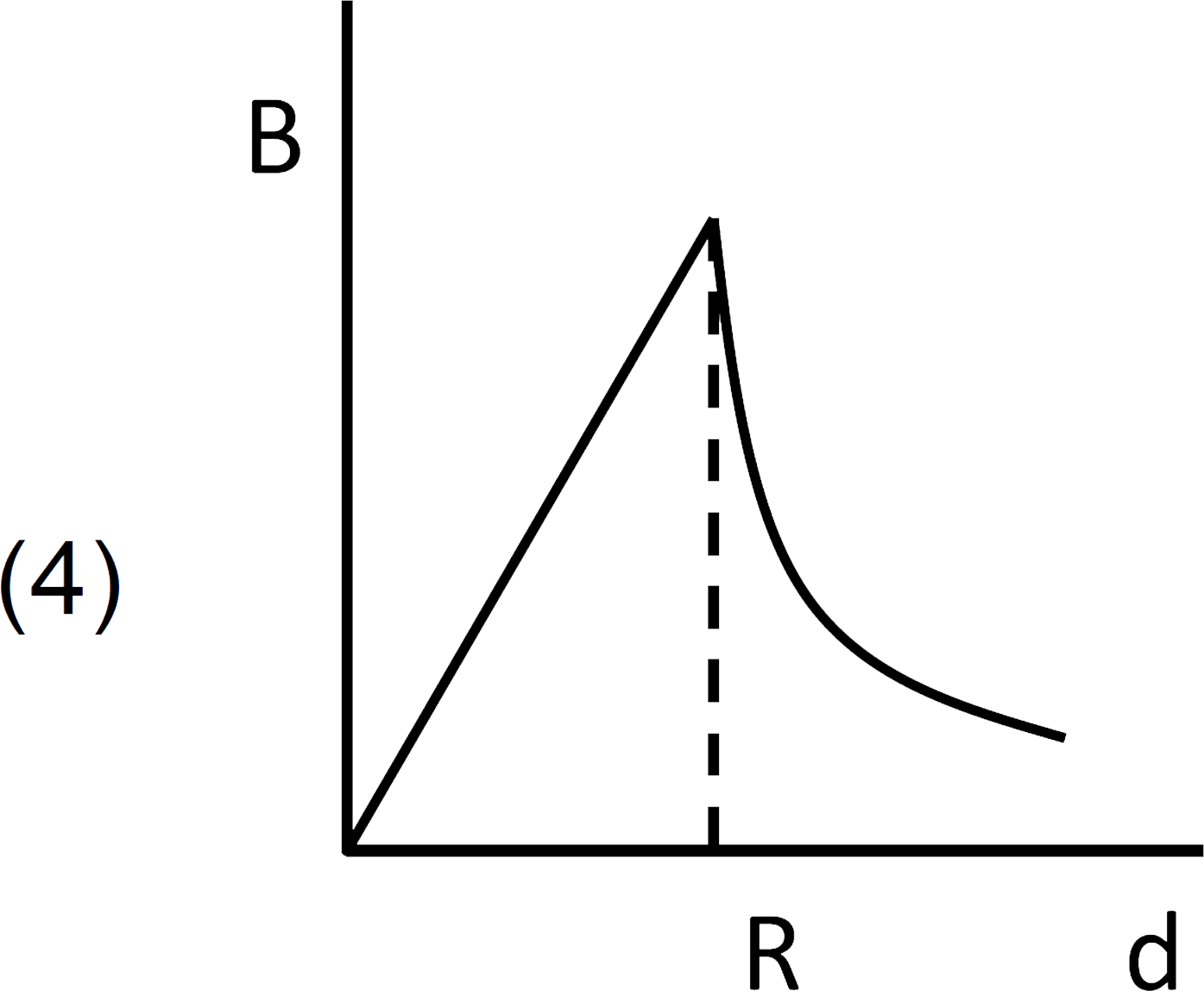
- Question 2 - Select One
A cylindrical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
A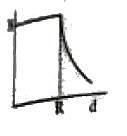 B
B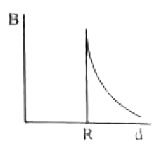 C
C D
D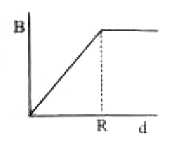
- Question 3 - Select One
A cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
A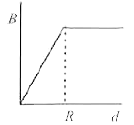 B
B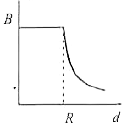 C
C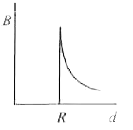 D
D
The magnitude of magnetic field at a distance 'r' from a long straight wire carrying a current I is given by B = …………………… .
View SolutionA long straight wire of radius R carries a steady current which is uniformly distributed through the cross-section of the wire. The magnitudes of the magnetic field at distance r1 and r2 from the centre of the wire are B1 and B2 respectively. Then
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View SolutionA long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
View SolutionA long straight wire of a circular cross section (radius a) carries a steady current 7 and the current / is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance from the centre of the wire?
View Solution

