A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
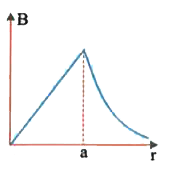
The correct Answer is:A
To solve the problem of determining the variation of the magnetic field B with distance r from the center of a long straight wire carrying a steady current I uniformly distributed across its circular cross-section, we can follow these steps:
Step 1: Identify the regions based on distance r
We need to consider two regions:
1. Inside the wire (where r<a)
2. Outside the wire (where r≥a)
Step 2: Apply Ampère's Law for the inside region (r<a)
For a point inside the wire, we can use Ampère's Law, which states:
∮→B⋅d→l=μ0Ienc
Where Ienc is the current enclosed by the Amperian loop of radius r.
The current density J is given by:
J=Iπa2
The enclosed current Ienc for a radius r is:
Ienc=J⋅A=J⋅πr2=Iπa2⋅πr2=Ir2a2
Now, applying Ampère's Law:
B(2πr)=μ0Ienc=μ0Ir2a2
Solving for B:
B=μ0Ir2πa2
Step 3: Apply Ampère's Law for the outside region (r≥a)
For points outside the wire, the entire current I is enclosed:
∮→B⋅d→l=μ0I
Thus:
B(2πr)=μ0I
Solving for B:
B=μ0I2πr
Step 4: Summarize the results
- For r<a:
B=μ0Ir2πa2
This indicates that B increases linearly with r inside the wire.
- For r≥a:
B=μ0I2πr
This indicates that B decreases with r outside the wire.
Step 5: Plot the results
- The plot for B vs r will show a linear increase for r<a and a hyperbolic decrease for r≥a.
Conclusion
The correct plot representing the variation of the magnetic field B with distance r from the center of the wire will show a linear increase up to the radius a and then a decrease as r increases beyond a.
---
We need to consider two regions:
1. Inside the wire (where r<a)
2. Outside the wire (where r≥a)
For a point inside the wire, we can use Ampère's Law, which states:
∮→B⋅d→l=μ0Ienc
Where Ienc is the current enclosed by the Amperian loop of radius r.
J=Iπa2
The enclosed current Ienc for a radius r is:
Ienc=J⋅A=J⋅πr2=Iπa2⋅πr2=Ir2a2
B(2πr)=μ0Ienc=μ0Ir2a2
Solving for B:
B=μ0Ir2πa2
For points outside the wire, the entire current I is enclosed:
∮→B⋅d→l=μ0I
Thus:
B(2πr)=μ0I
Solving for B:
B=μ0I2πr
- For r<a:
B=μ0Ir2πa2
This indicates that B increases linearly with r inside the wire.
- For r≥a:
B=μ0I2πr
This indicates that B decreases with r outside the wire.
- The plot for B vs r will show a linear increase for r<a and a hyperbolic decrease for r≥a.
The correct plot representing the variation of the magnetic field B with distance r from the center of the wire will show a linear increase up to the radius a and then a decrease as r increases beyond a.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 4
20 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 2(H.W) (FORCE ACTING A MOVING CHARGE IN MAGNETIC FIELD)
14 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View Solution
Knowledge Check
A long straight wire of a circular cross section (radius a) carries a steady current 7 and the current / is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance from the centre of the wire?
A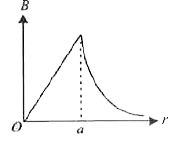 B
B C
C D
D
A long cylindrical wire carries a steady current which is uniformly distributed across its cross section. Which of the following is true?
AMagnetic field is zero at the centre.BElectric field is zero at the centre.CElectric field just outside the cylinder is zero.DMagnetic field just outside the cylinder is zero.The figure shows a long striaght wire of a circular cross-section (radius a) carrying steady current I.The current I is unifromly distributed across this distance a/2 and 2a from axis is
A2:1B1:2C4:1D1:1
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure show a long straight wire of a circular a cross-section with radius 'a' carrying steady curent I. The curent I is uniformaly distributed across this c ross -section.Calclulate the magnetic field in the regionr1<aandr2> a.
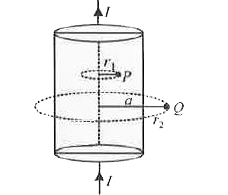
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
View SolutionWhich of the following graphs shows the variation of magnetic induction B with distance r from a long wire carrying current
View Solution
