The count rate of nuclear radiation coming from a radioactive sample containing ^128Ivarieswithtimeasfollows.<br>Timet(minute):0255075100<br>CountrateR(10^9 s^(-1)): 30 16 8.0 3.8 2.0
(a) plot In (R0/R)against t. (b) From the slope of the best straight line through the points,Find the decay constant λ.(c ) Calculate the half-life t_(1//2).
The correct Answer is:A, B, C
(a) Here we should take R0 at time t0
=30×109s−1
∴(i)In(R0R)=In(30×10930×109)=0
(ii)In(R0R2)=In(30×10916×109)=0.63
(iii) In (R_(0)/R_3) = In ((30 xx 10^(9))/(8 xx 10^(9))) = 1.35<br>(iv)In (R_0/R_4) = In ((30 xx 10^(9))/(3.8 xx (10^9))) = 2.06<br>(v)In (R_0/R_5) = In ((30 xx (10^9))/(2 xx (10^9))) = 2.7<br>(b):. The decay constant lambda = 0.028 min -1<br>:. The half life period <br>t_(1/2) = (0.693/lambda)<br>= (0.693/0.028) = 25 min .
Topper's Solved these Questions
Similar Questions
The rate of decay of a radioactive sample is R1 at time t1 and R2 at time t2. Calculate the mean liffe of sample.
View SolutionThe population of active nuclei in a sample of radioactive isotope has been plotted with time in figure. Look at the graph carefully and find the value of t2−t1. It is given that t0=50 munite.
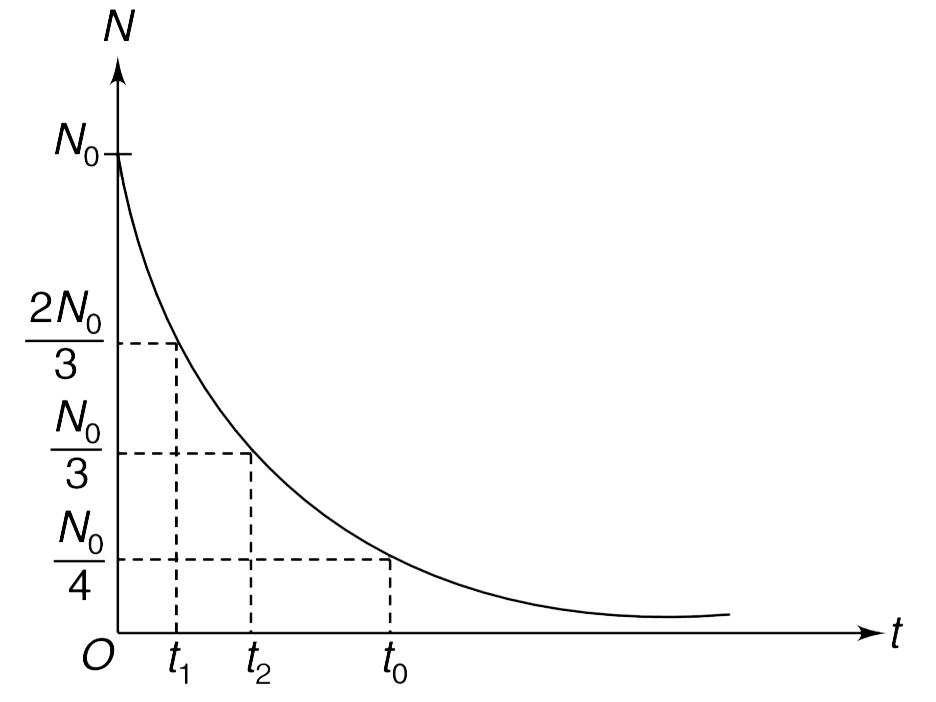
View Solution
Knowledge Check
The rate of decay of a radioactive sampel is given by R1 at time t1 and R2 at a later time. t2. The mean life of this radioactive sample is:
AT=R1R2×t2t1BT=t1−t2In(R2/R1)CT=t2−t1In(R2/R1)DT=In(R2/R1)t1−t2The current through a wire connected to a condenser varies with time as i=(2t+1)A the charge transport to the condenser from t=0 to t=5s is
A5CB55CC30CD60CThe charge flowing through a resistance R varies with time as Q=2t−8t2 . The total heat produced in the resistance is (for 0≤t≤18)
AR6 joulesBR3 joulesCR2 joulesDR joules
A nuclear reactor starts producing a radionuclide of half - life T at a constant rate R starting at time t = 0 The activity of the radionuclide at t = T is found to the A. Then R4 is
View SolutionThe count rate of a radioactive sample falls from 4.0×106s−1 to 1.0×106s−1 in 20 hours. What will be the count rate after 100 hours from beginning ?
View SolutionUsing a nuclear counter the count rate of emitted particles from a radioactive source is measured. At t = 0 seconds it was 25600 counts per second and t = 8 seconds it was 100 counts per second. The count rate observed, as counts per second, at t = 6 seconds is close to:
View SolutionAt time t=0N1 nuclei of decay constant λ1&N2 nuclei of decay constant λ2 are mixed. The decay rate of the mixture at time 't' is:
View SolutionAs radioactive substances undergo continuous decay, number of nuclei in a sample goes on decreasing. The time interval in which number of nuclei in a sample is reduced to half of its initial value is the half-life of the sample. The half-life is related to the decay constant by the relation.
T1/2=0.693λ
The average life of a sample is expressed by the relation
τ=1λ
The decay constant of a radioactive substance having half-life 2 minutes is
View Solution
