At time t=0N1 nuclei of decay constant λ1&N2 nuclei of decay constant λ2 are mixed. The decay rate of the mixture at time 't' is:
N1N2e−(λ1+λ2)t
(N1N2)e−(λ1−λ2)t
(N1λ1e−(λ1t)+N2λ2e−λ2t)
N1λ1N2λ2e−(λ1+λ2)t
The correct Answer is:C
Step by step video, text & image solution for At time t=0 N_(1) nuclei of decay constant lambda_(1)& N_(2) nuclei of decay constant lambda_(2) are mixed. The decay rate of the mixture at time 't' is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The decay constant (λ) for radioactive decay is independent of
View SolutionA radionuclide A1 with decay constant λ1 transforms into a radionuclide A2 with decay constant λ2. Assuming that at the initial moment the preparation contained only the radionuclide A1, find:
(a) the equation describing accumulation of the radionuclide A2 with time,
(b) the time interval after which the activity value.View Solution
Knowledge Check
- Question 1 - Select One
Uranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions ltbgt Numeber of the nuclei of nuclei C at time t isAN0[1+λ1λ2−λ1e−λ2t−λ2λ2−λ1e−λ1t]BN0[λ1λ2−λ1e−λ2t−λ2λ2−λ1e−λ1t]CN0λ1λ2−λ1(e−λ2t−e−λ1t)DN0[λ1λ2−λ1e−λ2t−λ2λ2−λ1e−λ1t−1] - Question 2 - Select One
Uranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions
Number of nuclei of B at any time t isAN0λ1λ2−λ1(eλ1t−eλ2t)BN0λ1λ2−λ1(e−λ1t−e−λ2t)CN0λ1λ2−λ1(e−λ1t−e−λ2t)DN0λ2λ2−λ1(e−λ1t+e−λ2t) - Question 3 - Select One
Uranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions
The graph N1,N2 and N3 with time can be best represent byA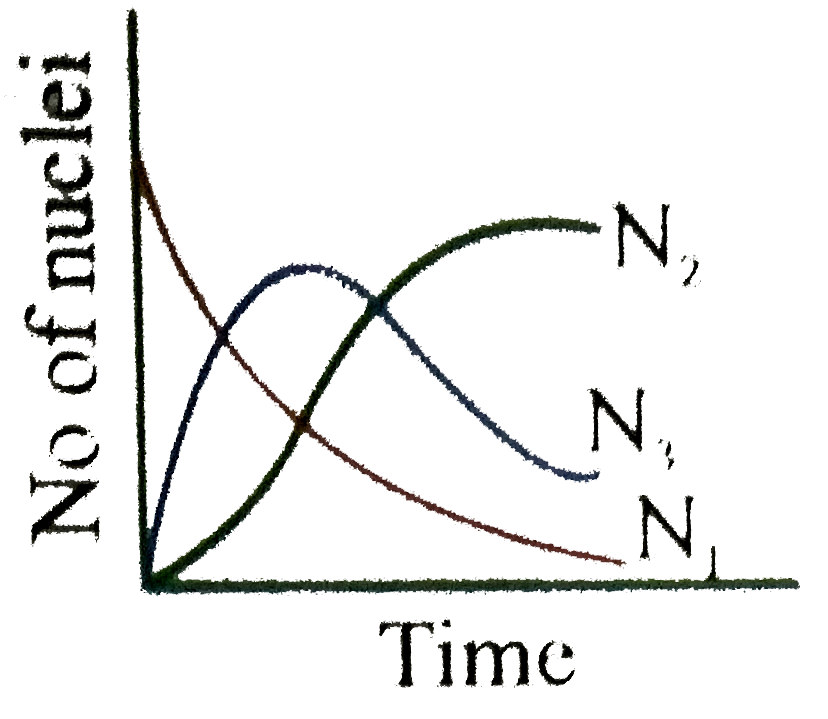 B
B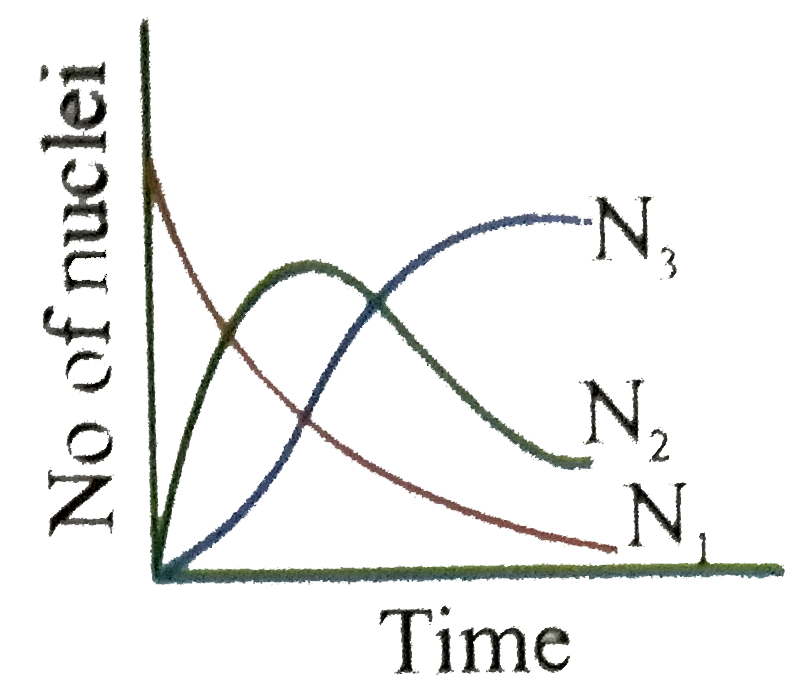 C
C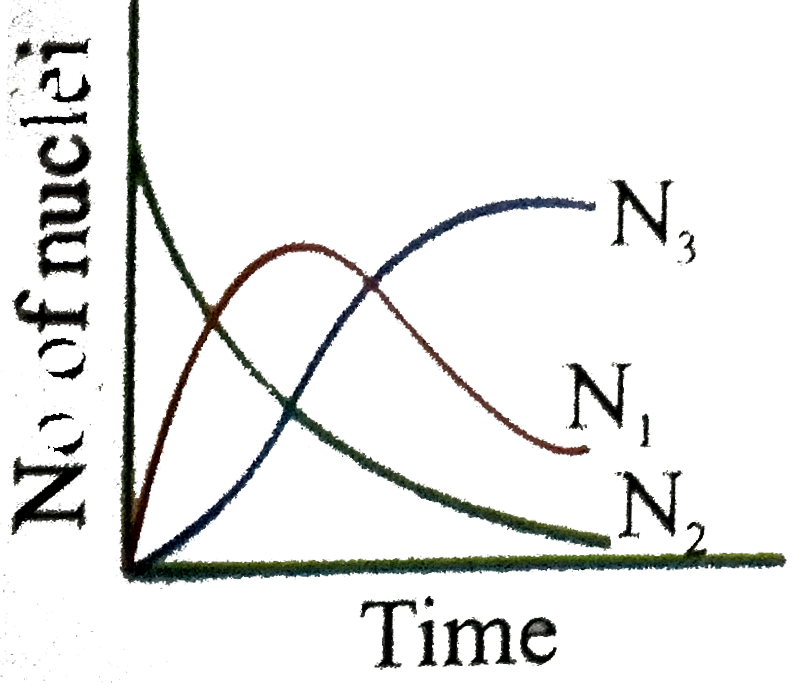 D
D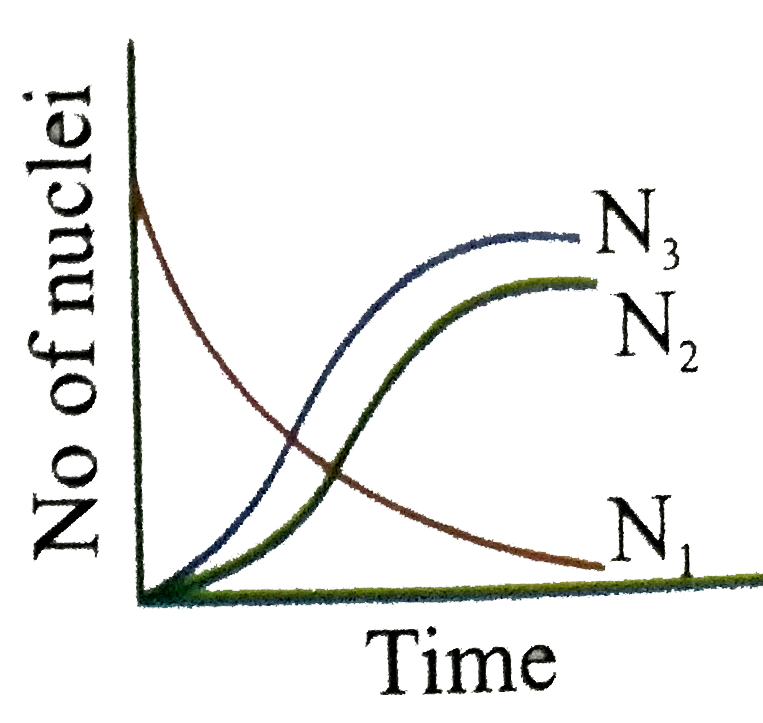
A radioactive substance A having N0 active nuclei at t=0, decays to another radioactive substance B with decay constant λ1. B further decays to a stable substance C with decay constant λ2. (a) Find the number of nuclei of A,B and C time t. (b) What should be the answer of part (a) if λ1>>λ2 and λ1<<λ2
View SolutionA radioactive element A of decay constant λA decays into another radioactive element B of decay constant λB. Initially the number of active nuclei of A was N0 and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In 2/λA. The maximum number of active nuclei of B is
View SolutionNucleus A decays to B with decay constant λ1 and B decays to C with decay constant λ2. Initially at t=0 number of nuclei of A and B are 2N0 and N0 respectively. At t=to, no. of nuclei of B is 3N02 and nuclei of B stop changing. Find t0?
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View SolutionA radioacitve nucleus is being produced at a constant rate α per second. Its decay constant is λ. If N0 are the number of nuclei at time t=0, then maximum number of nuceli possible are .
View Solution

