The count rate of nuclear radiation coming from a radioactive sample containing varies with time as follows.
Time t (minute): 0 25 50 75 100
Count rate : 30 16 8.0 3.8 2.0
(a) plot against t. (b) From the slope of the best straight line through the points,Find the decay constant .(c ) Calculate the half-life .
The correct Answer is:A, B, C
(a) Here we should take at time
(ii)
(iii) In (R_(0)/R_3) = In ((30 xx 10^(9))/(8 xx 10^(9))) = 1.35In (R_0/R_4) = In ((30 xx 10^(9))/(3.8 xx (10^9))) = 2.06In (R_0/R_5) = In ((30 xx (10^9))/(2 xx (10^9))) = 2.7:. The decay constant lambda = 0.028 min -1:. The half life period t_(1/2) = (0.693/lambda)= (0.693/0.028) = 25 min .
Topper's Solved these Questions
- THE NUCLEOUSBook:HC VERMA ENGLISHChapter:THE NUCLEOUSExercise:Short answer
Explore 12 Videos
- THE NUCLEOUSBook:HC VERMA ENGLISHChapter:THE NUCLEOUSExercise:Objective 2
Explore 10 Videos
- SPEED OF LIGHTBook:HC VERMA ENGLISHChapter:SPEED OF LIGHTExercise:Question for short Answer
Explore 5 Videos
- THE SPECIAL THEORY OF RELATIVITYBook:HC VERMA ENGLISHChapter:THE SPECIAL THEORY OF RELATIVITYExercise:Short answer
Explore 2 Videos
Similar Questions
A nuclear reactor starts producing a radionuclide of half - life T at a constant rate R starting at time t = 0 The activity of the radionuclide at t = T is found to the A. Then R4 is
View SolutionUsing a nuclear counter the count rate of emitted particles from a radioactive source is measured. At t=0 it was 1600 counts per second and t = 8 seconds it was 100 counts per second. The count rate observed, as counts per seconds, at t=6, seconds is close to :
View Solution
Knowledge Check
The count rate of a radioactive sample falls from 4.0×106s−1 to 1.0×106s−1 in 20 hours. What will be the count rate after 100 hours from beginning ?
A3.91×103s−1B3.91×102s−1C3.91×104s−1D3.91×106s−1The graph of a line in the xy-plane has slope 12 and contains the point (0,7). The graph of a seconds line passes through the points (0,0)and(−1,3). If the two lines intersect at the point (r,s), what is the value of r+s?
A−3B−2C2D4
At time t=0N1 nuclei of decay constant λ1&N2 nuclei of decay constant λ2 are mixed. The decay rate of the mixture at time 't' is:
View SolutionThe time constant of an LR circuit is 40 ms. The circuit is connected at t= 0 and the steady state current is found ot be 2.0 A. Find the current at (a) t= 10 ms (b) t =20ms, (c ) t =100ms and (d) t = 1 s.
View SolutionA stable nuclei C is formed from two radioactive nuclei A and B with decay constant of λ1 and λ2 respectively. Initially, the number of nuclei of A is N0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.
View SolutionRate constant k of a reaction varies with temperature according to the equation
logk = constant −Ea2.303R(1T)
where Ea is the energy of activation for the reaction . When a graph is plotted for log k versus 1T , a straight line with a slope - 6670 K is obtained. Calculate the energy of activation for this reaction
View SolutionA particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
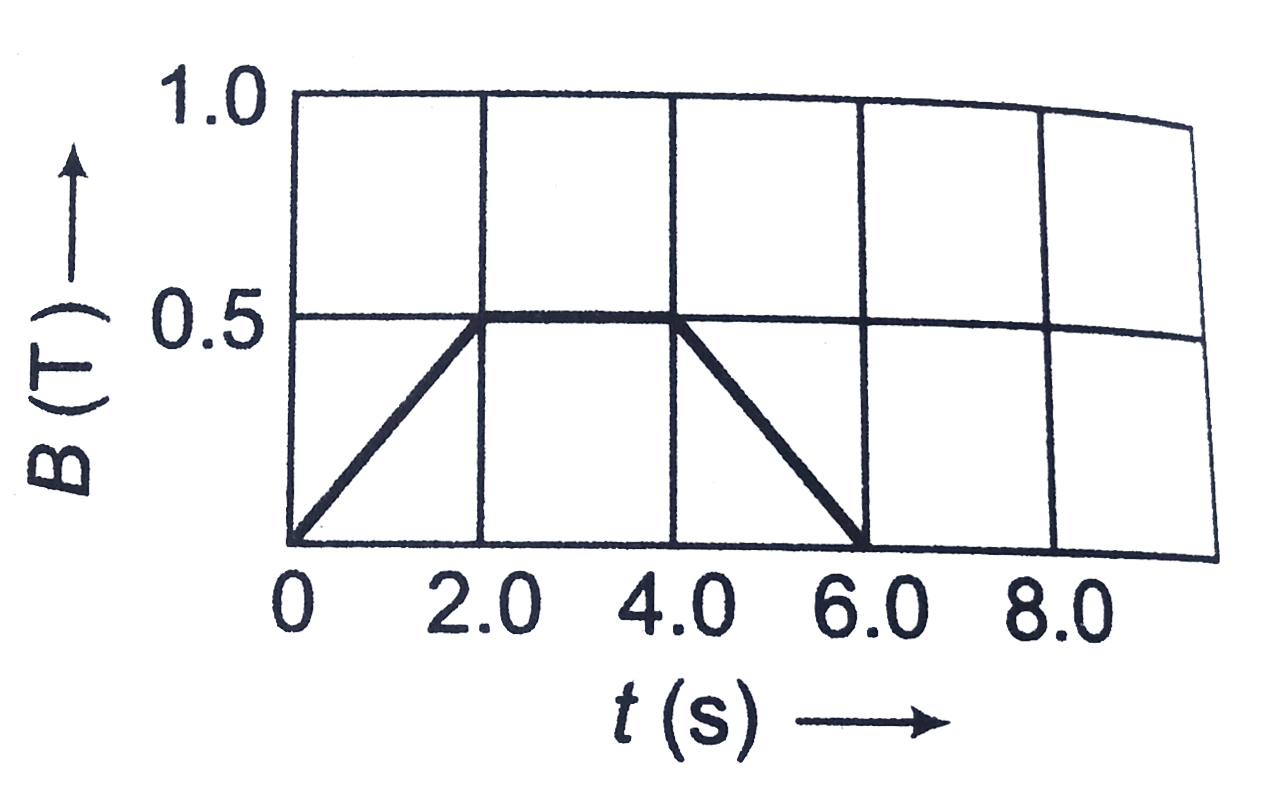
View SolutionThe magnetic field through a single loop of wire, 12cm in radius and of 8.5Ω resistance, changes with time as shown in figure. Calculate the emf in the loop as a function of time. Consider the time intervals
(a) t=0 to t=2.0s (b) t=2.0s to t=4.0s (c) t=4.0s to t=6.0s.
The magnetic field is perpendicular to the plane of the loop.
View Solution
