A particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
12m
16m
18m
20m
The correct Answer is:A
To find the total distance covered by the particle from t=0 to t=6 seconds, we start with the given velocity function:
v(t)=8−2t(in m/s)
Step 1: Determine when the particle changes direction
First, we need to find out if the particle changes direction during the interval from t=0 to t=6 seconds. This occurs when the velocity v(t) becomes zero.
Set the velocity to zero:
8−2t=0
Solving for t:
2t=8⟹t=4 seconds
Step 2: Calculate the distance for each segment
Now we will calculate the distance covered in two segments: from t=0 to t=4 seconds (when the particle is moving in one direction) and from t=4 to t=6 seconds (when the particle is moving in the opposite direction).
Segment 1: From t=0 to t=4
We need to find the displacement during this time. We can integrate the velocity function:
Displacement=∫40(8−2t)dt
Calculating the integral:
=∫408dt−∫402tdt
Calculating each integral:
=8t∣∣∣40−2⋅t22∣∣∣40
Evaluating the limits:
=8(4)−(42)=32−16=16 meters
Segment 2: From t=4 to t=6
Now we calculate the displacement from t=4 to t=6:
Displacement=∫64(8−2t)dt
Calculating the integral:
=∫648dt−∫642tdt
Calculating each integral:
=8t∣∣∣64−2⋅t22∣∣∣64
Evaluating the limits:
=8(6)−8(4)−(62−42)=48−32−(36−16)=16−20=−4 meters
Since distance cannot be negative, we take the absolute value:
Distance=4 meters
Step 3: Total distance covered
Now, we add the distances from both segments:
Total Distance=16 meters+4 meters=20 meters
Thus, the total distance covered by the particle from t=0 to t=6 seconds is:
20 meters
First, we need to find out if the particle changes direction during the interval from t=0 to t=6 seconds. This occurs when the velocity v(t) becomes zero.
Now we will calculate the distance covered in two segments: from t=0 to t=4 seconds (when the particle is moving in one direction) and from t=4 to t=6 seconds (when the particle is moving in the opposite direction).
We need to find the displacement during this time. We can integrate the velocity function:
Now we calculate the displacement from t=4 to t=6:
Now, we add the distances from both segments:
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
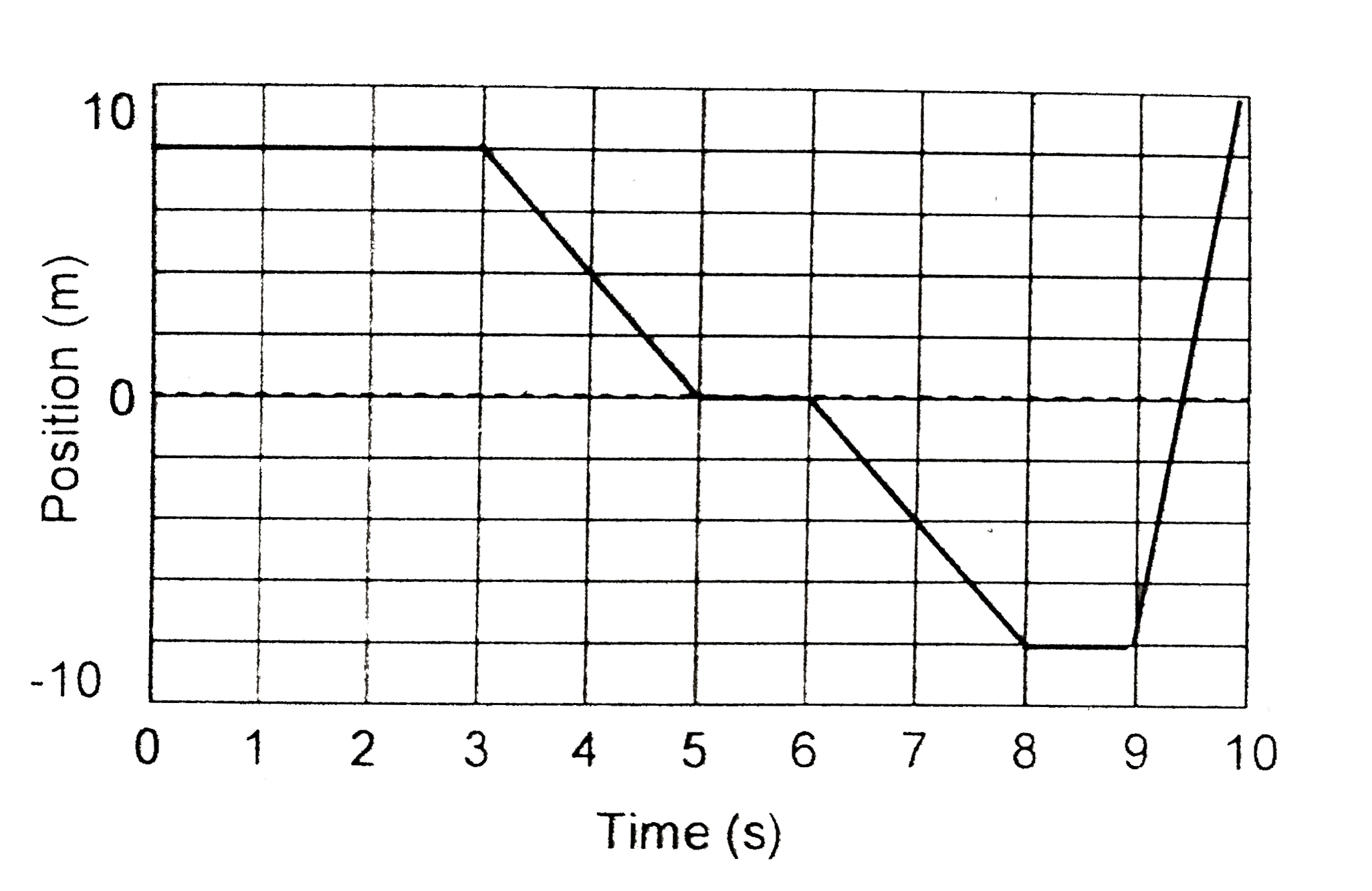
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionA particle is moving in a straight line. Its displacement at time t is given by s(Inm)=4t2+2t, then its velocity and acceleration at time t=12 second are
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f. If the sum of the distances travelled in tthand(t+1)th seconds is 100cm, then its velocity after t seconds, in cm/s, is.
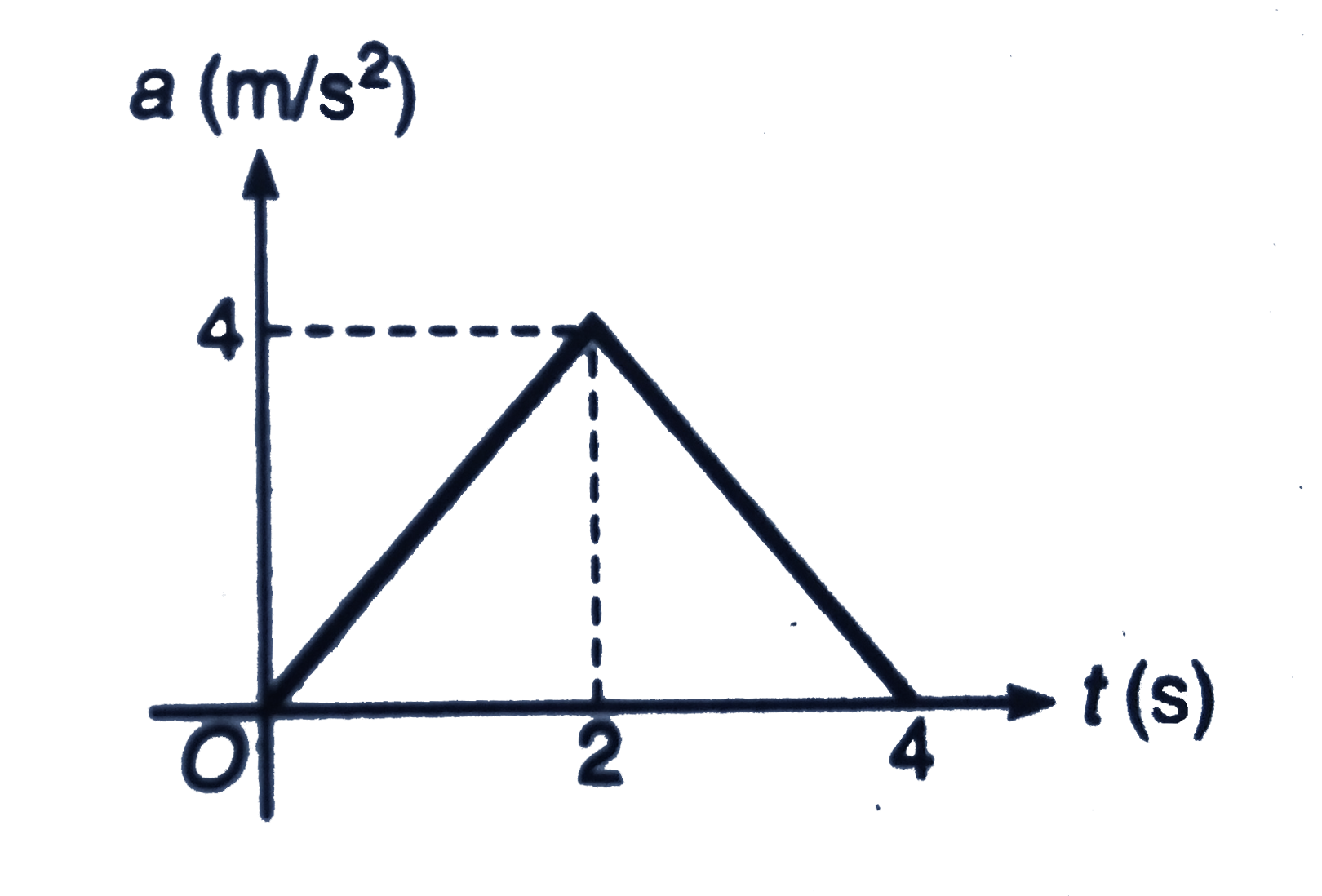
View SolutionAccleration-time graph of a particle moving in a straight line is as shown in Fig. Velocity of particle at time t=0 is 2m/s. Find the velocity at the end of fourth second.
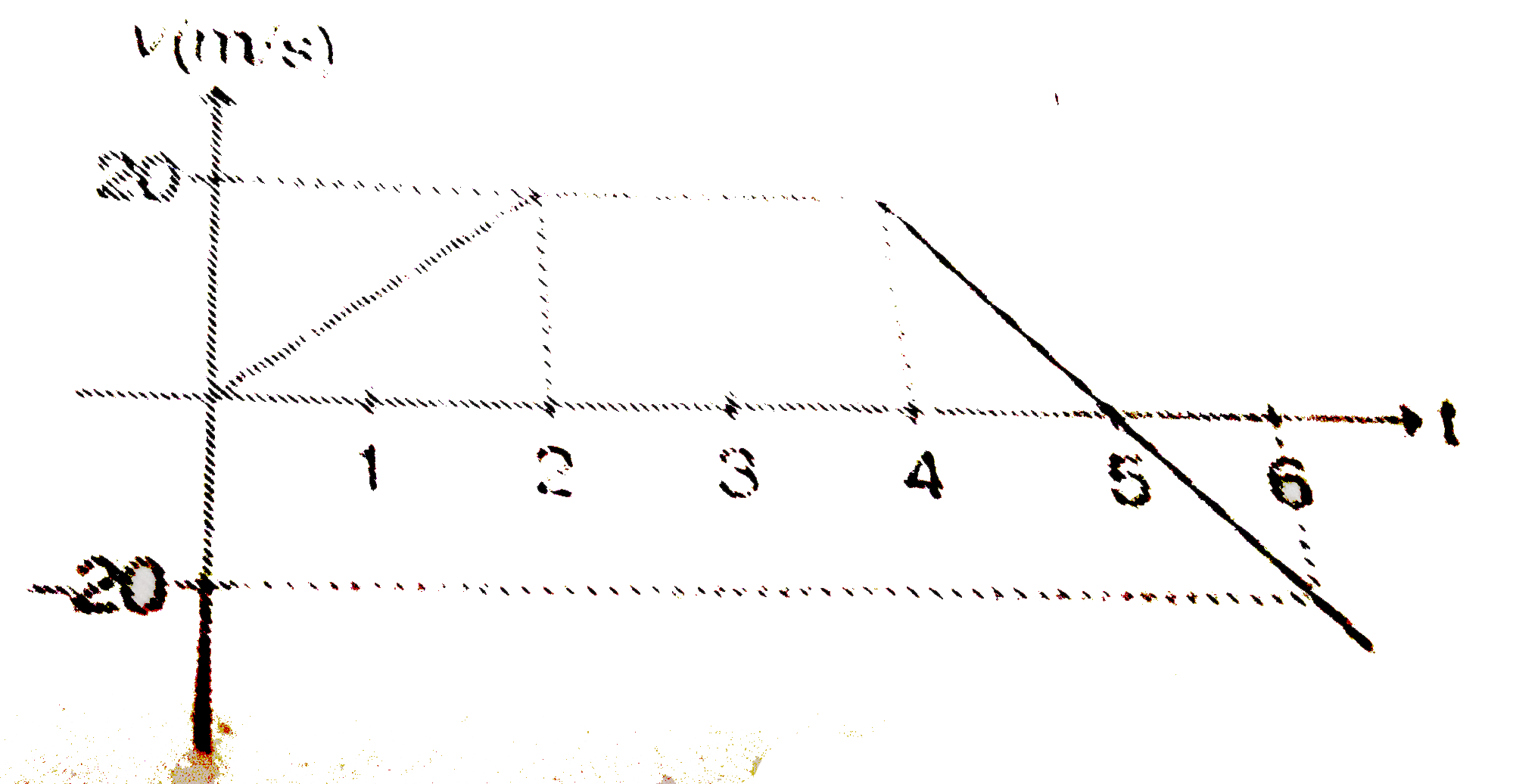
View SolutionFigure shows the velocity time graph for a particle travelling along a straight line. The magnitude of average velocity (in m/s) of particle during the time interval from t=0 to t=6s is 10α. Find the value of α.
View SolutionIf a point is moving in a line so that its velocity at time t is proportional to the square of the distance covered, then its acceleration at time t varies as
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionA particle moving in a straight line has its velocit varying with time according to relation v=t2−6t+8(m/s) where t is in seconds. The CORRECT statement(s) about motion of this particle is/are:-
View Solution
