The critical angle of light from medium A to medium B is θ. The speed of light in medium A is v. the speed of light in medium B is
vsinθ
vcosθ
vsinθ
vcosθ
The correct Answer is:A
To find the speed of light in medium B given the critical angle θ and the speed of light in medium A (v), we can follow these steps:
1. Understanding Critical Angle: The critical angle θ is defined as the angle of incidence in medium A at which light is refracted along the boundary between the two media. Beyond this angle, total internal reflection occurs.
2. Using Snell's Law: According to Snell's Law, the relationship between the angles and the refractive indices of the two media is given by:
nAsin(θ)=nBsin(90∘)
Since sin(90∘)=1, we can simplify this to:
nAsin(θ)=nB
3. Refractive Index Relation: The refractive index n of a medium is defined as:
n=cv
where c is the speed of light in vacuum and v is the speed of light in the medium. Therefore, we can express the refractive indices of the two media as:
nA=cvAandnB=cvB
4. Substituting Refractive Indices: Substituting the expressions for nA and nB into the equation from Snell's Law gives us:
cvAsin(θ)=cvB
5. Cancelling c: Since c appears on both sides of the equation, we can cancel it out:
sin(θ)vA=1vB
6. Rearranging for vB: Rearranging the equation to solve for vB gives:
vB=vAsin(θ)
7. Final Expression: Since we are given that the speed of light in medium A is v, we can replace vA with v:
vB=vsin(θ)
Conclusion:
The speed of light in medium B is given by:
vB=vsin(θ)
nAsin(θ)=nBsin(90∘)
Since sin(90∘)=1, we can simplify this to:
nAsin(θ)=nB
n=cv
where c is the speed of light in vacuum and v is the speed of light in the medium. Therefore, we can express the refractive indices of the two media as:
nA=cvAandnB=cvB
cvAsin(θ)=cvB
sin(θ)vA=1vB
vB=vAsin(θ)
vB=vsin(θ)
The speed of light in medium B is given by:
vB=vsin(θ)
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
Knowledge Check
Critical angle for light going from medium (i) to (ii) is θ . The speed of light in medium (i) is v then speed in medium (ii) is
Av(1−cosθ)BvsinθCvcosθDv(1−sinθ)Consider two adjacent transparent media. The speed of light in medium 1 is v1, and the speed of light in medium 2 is v2. If v1<v2, then total internal reflection will occur at the interface between these media if a beam of light is
Aincident in medium 1 and strikes the interface at an angle of incidence greater than sin−1(v1/v2).Bincident in medium 1 and strikes the interface at an angle of incidence greater than sin−1(v2/v1).Cincident in medium 2 and strikes the interface at an angle of incidence greater than sin−1(v1/v2).Dincident in medium 2 and strikes the interface at an angle of incidence greater than sin−1(v2/v1).
If critical angle for TIR from medium to vacuum is 45 deg then velocity of light in medium
View SolutionThe speed of light in an isotropic medium depends on
View SolutionThe dispersion of light in a medium implies that :
View SolutionFind the speed of light in medium 'a' if speed of light in medium 'b' is c/3, where c =speed of light in vacuum and light refracts from medium 'a' to medium 'b' making 45∘ and 60∘, respectively, with the normal.
View SolutionThe time required for the light to go from A to B, when a ray of lilght goes from point A in a medium where the speed of light is v1 to a point B in a medium where the speed of light is v2 as shown in figure is
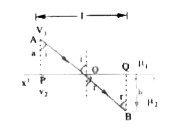
View SolutionThe refractive index of a medium 'x' with respect to a medium 'y' is 23 and the refractive index of medium 'y' with respect to medium 'z' is 43. Find the refractive index of medium 'z' with respect to medium 'x' . If the speed of light in medium 'x' is 3×108ms−1, Calculate the speed of light in medium 'y'.
View Solution
