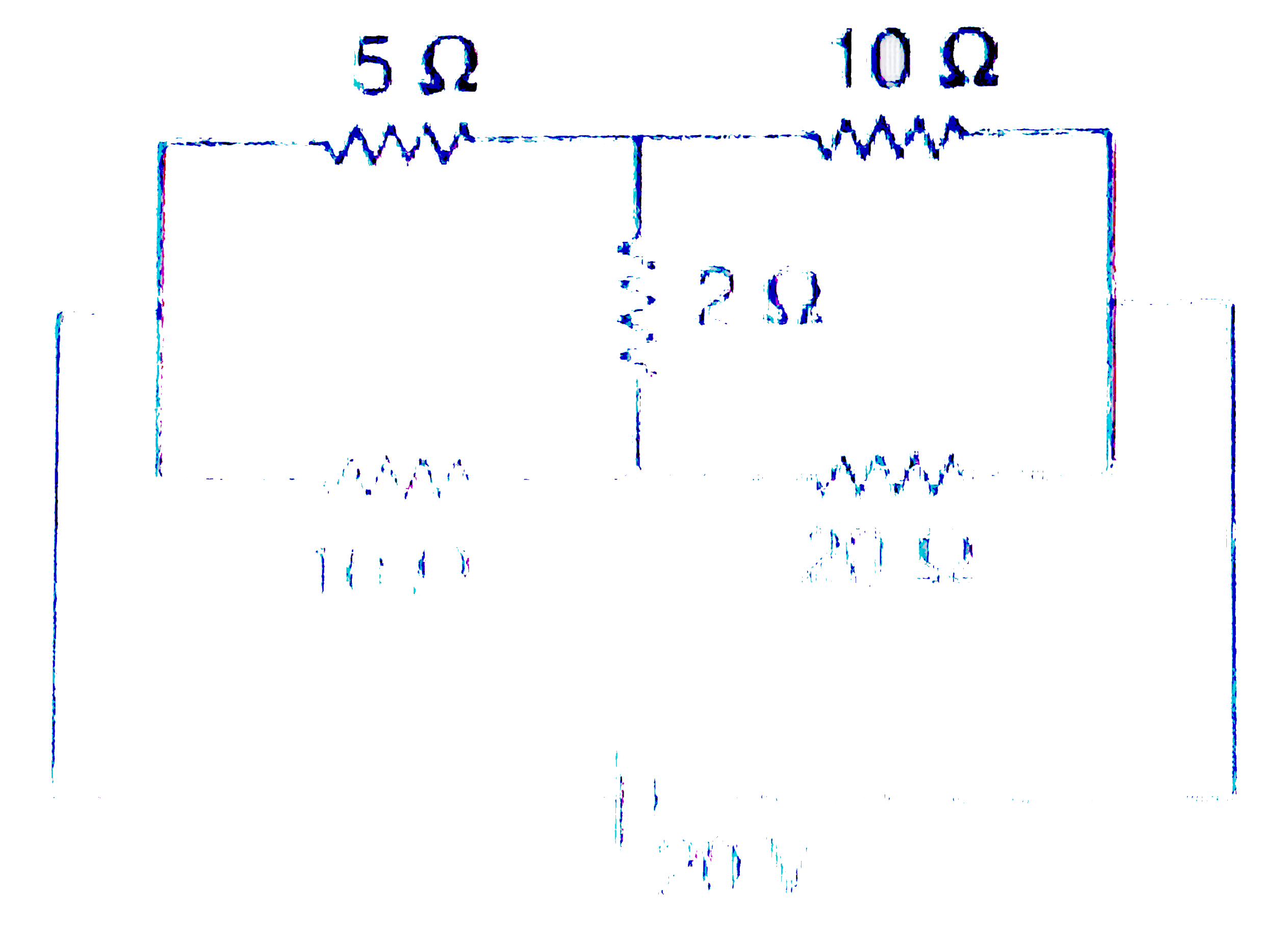
the current developed in a real conductor is given where V is the potential difference acid the conductor. When it is connected with resistance of in series with a battery of 6 volt shown in the figure , the power developed in conductor is twice the power generated in resistance of . find the value of
The correct Answer is:5
Step by step video, text & image solution for the current developed in a real conductor is given I=aV^(1//2), where V is the potential difference acid the conductor. When it is connected with resistance of R Omega in series with a battery of 6 volt shown in the figure , the power developed in conductor is twice the power generated in resistance of R Omega . find the value of R."["a=0.2 A "Volt"^(-1//2)"]" by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Current P through a certain non-metallic rod is given as i0=0.2V32 where V is potential difference across it. The rod is connected in series with a resistance to a 12 volt ideal bettery. What should be resistance ( in Ω) so that power dissipated in the resistance is twice that of rod.
View SolutionA current of 0.2A flows through a conductor of resistance 4.5Ω. Calculate the potential difference at the ends of the conductor.
View Solution
Knowledge Check
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A700ΩB800ΩC900ΩD100ΩIn the circuit shown in figure, power developed across 1Ω,2Ω and 3Ω resistance are in the ratio of
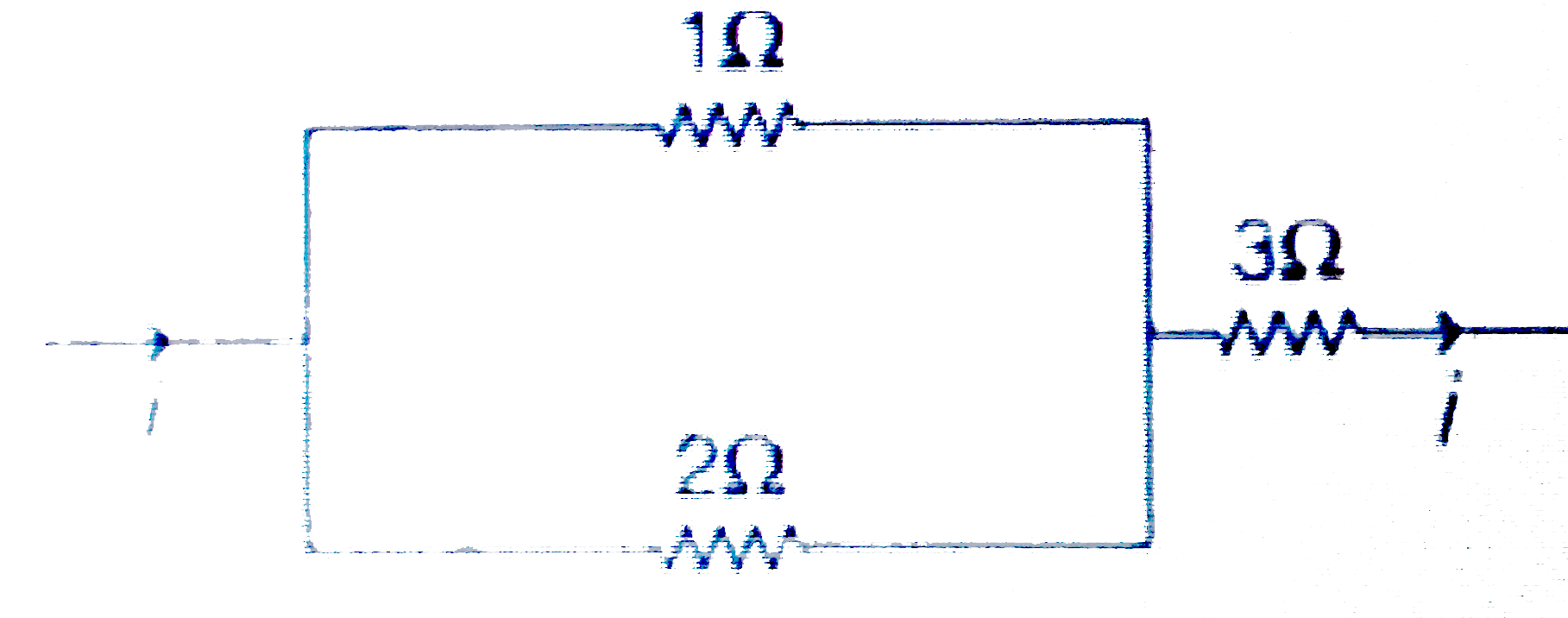 A1:2:3B4:2:27C6:4:9D2:1:27
A1:2:3B4:2:27C6:4:9D2:1:27Two batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
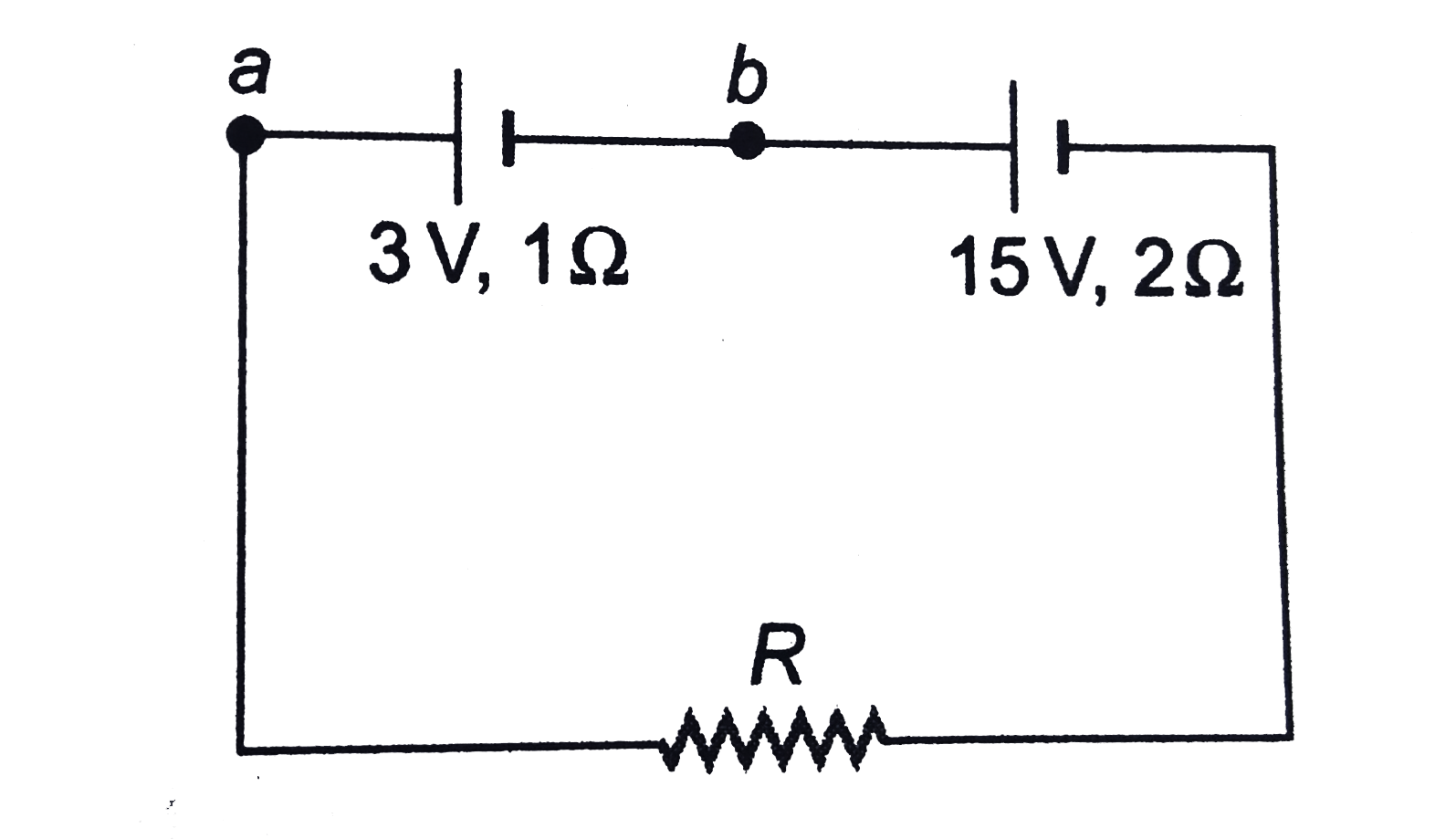 A5B7C3D1
A5B7C3D1
A potential difference of 10 V is applied across a conductor of resistance 1kΩ. Find the number of electrons flowing through the conductor in 5 minutes.
View SolutionA battery of emf 10 V is connected with a load resistance of 50 Omega the total power delivered by the battery is 2 W. If load resistance is replaced by R then power delivered is 4 W, the value of R is
View SolutionA conductor of resistance 25Ω of diameter 0.2 mm is connected to a battery of 200 V . Calculate the current density for the conductor.
View SolutionThe resistance of two conductors in series is 40Ω and their resistance becomes 6.4Ω, when connected in parallel. Find the resistance of individual conductors.
View SolutionIf the potential difference across the ends of a conductor is i volt and the current flowing through the conductor is 1 ampere,the resistance of the conductor?
View Solution
