The density of silver is 10.5 g/cc and its atomic mass is approximately 108 g . Assume each atom contributes one free electron and calcute the number of free electrons per unit volume for the silver. Resistivity of the silver is 1.6×10−8Ωm.
What potential difference must be applied across the silver wire of length 0.1 m and area of cross section 1mm2 so that a current of 2A flows through it ? what will be the current density for the wire and drift speed of electrons ?
To solve the problem step by step, we can break it down into parts as follows:
Step 1: Calculate the number of free electrons per unit volume for silver.
1. Given Data:
- Density of silver (ρ) = 10.5 g/cc = 10.5 x 10^3 kg/m³ (since 1 g/cc = 1000 kg/m³)
- Atomic mass of silver (M) = 108 g/mol = 0.108 kg/mol
- Avogadro's number (N_A) = 6.022 x 10²³ atoms/mol
2. Calculate the number of moles of silver in 1 m³:
Number of moles=DensityAtomic mass=10.5×103 kg/m30.108 kg/mol≈97222.22 mol/m3
3. Calculate the number of free electrons per unit volume (n):
Since each atom contributes one free electron,
n=Number of moles×NA=97222.22 mol/m3×6.022×1023 atoms/mol≈5.85×1028 electrons/m3
Step 2: Calculate the potential difference required across the silver wire.
1. Given Data:
- Length of wire (L) = 0.1 m
- Area of cross-section (A) = 1 mm² = 1 \times 10^{-6} m²
- Current (I) = 2 A
- Resistivity of silver (ρ) = 1.6 x 10^{-8} Ωm
2. Calculate the resistance (R) of the wire:
R=ρLA=1.6×10−8 Ωm×0.1 m1×10−6 m2=1.6×10−2 Ω
3. Calculate the potential difference (V) using Ohm's law (V = I * R):
V=I×R=2 A×1.6×10−2 Ω=3.2×10−2 V=0.032 V
Step 3: Calculate the current density (J) for the wire.
1. Using the formula for current density:
J=IA=2 A1×10−6 m2=2×106 A/m2
Step 4: Calculate the drift speed (V_d) of electrons.
1. Using the formula for drift speed:
Vd=In⋅A⋅e
where e (charge of an electron) = 1.6×10−19 C.
2. Substituting the values:
Vd=2 A(5.85×1028 electrons/m3)⋅(1×10−6 m2)⋅(1.6×10−19 C)
Vd≈2(5.85×1028)⋅(1×10−6)⋅(1.6×10−19)≈2.16×10−4 m/s
Summary of Results:
- Number of free electrons per unit volume: n≈5.85×1028 electrons/m3
- Potential difference required: V≈0.032 V
- Current density: J≈2×106 A/m2
- Drift speed of electrons: Vd≈2.16×10−4 m/s
- Density of silver (ρ) = 10.5 g/cc = 10.5 x 10^3 kg/m³ (since 1 g/cc = 1000 kg/m³)
- Atomic mass of silver (M) = 108 g/mol = 0.108 kg/mol
- Avogadro's number (N_A) = 6.022 x 10²³ atoms/mol
Number of moles=DensityAtomic mass=10.5×103 kg/m30.108 kg/mol≈97222.22 mol/m3
Since each atom contributes one free electron,
n=Number of moles×NA=97222.22 mol/m3×6.022×1023 atoms/mol≈5.85×1028 electrons/m3
- Length of wire (L) = 0.1 m
- Area of cross-section (A) = 1 mm² = 1 \times 10^{-6} m²
- Current (I) = 2 A
- Resistivity of silver (ρ) = 1.6 x 10^{-8} Ωm
R=ρLA=1.6×10−8 Ωm×0.1 m1×10−6 m2=1.6×10−2 Ω
V=I×R=2 A×1.6×10−2 Ω=3.2×10−2 V=0.032 V
J=IA=2 A1×10−6 m2=2×106 A/m2
Vd=In⋅A⋅e
where e (charge of an electron) = 1.6×10−19 C.
Vd=2 A(5.85×1028 electrons/m3)⋅(1×10−6 m2)⋅(1.6×10−19 C)
Vd≈2(5.85×1028)⋅(1×10−6)⋅(1.6×10−19)≈2.16×10−4 m/s
- Number of free electrons per unit volume: n≈5.85×1028 electrons/m3
- Potential difference required: V≈0.032 V
- Current density: J≈2×106 A/m2
- Drift speed of electrons: Vd≈2.16×10−4 m/s
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS
71 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n
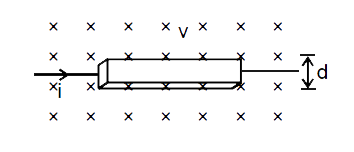
Find the drift velocity v of the electrons.
View SolutionA silver wire of length 2m and radius 1mm is joined in series with an iron wire of length "4m" and radius "3mm" and a current is passed through the wires. The ratio of the current density in the silver and iron wires is
View Solution
Knowledge Check
The resistivity of a potentiometer wire is 40×10−8Ω−m and its area of cross section is 8×10−6m2. If 0.2 A current is flowing through the wire the potential gradient will be
A10−2VmB10−1VmC3.2×10−2VmD1VmWhen 5 V potential difference is applied across a wire of length 0.1 m, the drift speed of electrons is 2.5×10−4ms−1. If the electron density in the wire is 8×1028m−3, the resistivity of the material is close to :
A1.6×10−6ΩmB1.6×10−5ΩmC1.6×10−8ΩmD1.6×10−7Ωm
A current of 1.34A exists in a copper wire of cross-section 1.0mm2. Assuming each copper atom contributes one free electron. Calculate the drift speed of the free electrons in the wire. The density of copper is 8990 kg/m3 and atomic mass=63.50.
View SolutionWhen 5 V potential difference is applied across a wire of length 0.1 m. The drift speed of electrons is 2.5×10−4ms−1. If the electron density in the wire is 8×1028m−3, calculate the resistivity of the material of wire
View SolutionAssuming that there is one free electron per atom in copper, determine the number of free electrons in 1metre3 volume of copper. Density of copper is 8.9×103kgm−3 and atomic weight 63.5. (Avogadro's number, N=6.02×1026 per kg-atom).
View SolutionThe density of silver having atomic mass 107. 9 u is 10.5 gcm−3
If its crystalline structure is fcc find the edge length and radius of silver atom.
View SolutionThe current in a metal wire of cross-sectional area 10−6m2 is 1.6A .If the free electron density of the metal is 8×1028m−3 then the drift speed of electrons is
View SolutionWe know that copper is a conductor of electricity due to presence of free electrons in it. Assume that on an average each copper atom provides one free electron. Find the number of free electrons per unit valume of copper. The density of copper is approximately 9,000 kg /m3 and its atomic mass is 63.5 u.
View Solution
