The density $ρ$ of a liquid varies with depth h from the free surface as $ρ = k h$ . A small body of density $ρ_{1}$ is released from the surface of liquid. The body will

come to a momentary rest at a depth $2 ρ_{1} / k$ from the free surface

execute S.H.M. about a point at a depth $ρ_{1} / k$ from the surface

execute S.H.M. of amplitude $ρ_{1} / k$

all of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Density of a liquid varies with depth as $ρ = α$ h. A small ball of density $ρ_{0}$ is released from the free surface of the liquid. Then
Athe ball will execute SHM of amplitude $\frac{ρ_{0}}{α}$
Bthe mean position of the ball will be at a depth $\frac{ρ_{0}}{2 α}$
Cthe ball will sink to a maximum depth of $\frac{ρ_{0}}{α}$
DThe ball sink to a maximum depth of $\frac{ρ_{0}}{α}$
A ball of density $ρ$ is released from deep inside of a liquid of density $2 ρ$ . It will move up
Awith an increasing acceleration
Bwith a decreasing acceleration
Cwith a constant acceleration
Dwith zero acceleration
A uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as $ρ = ρ_{0} (1 + \frac{h}{h_{0}})$ where h is depth from free surface. Density of sphere $σ$ will be :

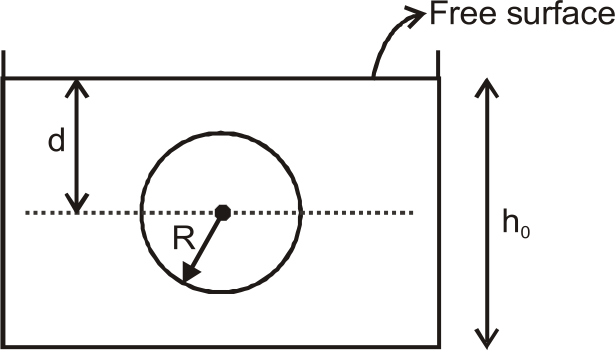A $σ = ρ_{0} (1 + \frac{d}{2 h_{0}})$
B $σ = ρ_{0} (1 - \frac{d}{2 h_{0}})$
C $σ = ρ_{0} (1 + \frac{2 d}{h_{0}})$
D $σ = ρ_{0} (1 + \frac{d}{h_{0}})$