A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
h
a
ρ
g
The correct Answer is:C
To solve the problem, we need to analyze the situation described in the question. We have a liquid of density ρ in a vessel, and a hole is made at a certain depth below the surface. We want to find out which quantity the speed of the liquid coming out of the hole is independent of.
1. Understanding the Situation:
- We have a liquid with density ρ filled to a height H in a container.
- A hole with cross-sectional area A is located at a depth h below the liquid's surface.
2. Applying Torricelli's Law:
- According to Torricelli's law, the speed of efflux v of a liquid through a hole under the influence of gravity can be expressed as:
v=√2gh
- Here, g is the acceleration due to gravity, and h is the height of the liquid column above the hole.
3. Identifying the Variables:
- The speed v depends on:
- g (acceleration due to gravity)
- h (height of the liquid column)
- The cross-sectional area of the hole A and the cross-sectional area of the container Ac can also influence the flow rate but do not directly affect the speed of efflux.
4. Analyzing the Independence:
- Now, we need to identify which quantity the speed v is independent of.
- The density ρ of the liquid does not appear in the formula for v. This means that the speed of the liquid coming out of the hole does not depend on the density of the liquid.
5. Conclusion:
- Therefore, the speed of the liquid coming out of the hole is independent of the density ρ.
Final Answer:
The speed of the liquid coming out of the hole is independent of the density ρ.
- We have a liquid with density ρ filled to a height H in a container.
- A hole with cross-sectional area A is located at a depth h below the liquid's surface.
- According to Torricelli's law, the speed of efflux v of a liquid through a hole under the influence of gravity can be expressed as:
v=√2gh
- Here, g is the acceleration due to gravity, and h is the height of the liquid column above the hole.
- The speed v depends on:
- g (acceleration due to gravity)
- h (height of the liquid column)
- The cross-sectional area of the hole A and the cross-sectional area of the container Ac can also influence the flow rate but do not directly affect the speed of efflux.
- Now, we need to identify which quantity the speed v is independent of.
- The density ρ of the liquid does not appear in the formula for v. This means that the speed of the liquid coming out of the hole does not depend on the density of the liquid.
- Therefore, the speed of the liquid coming out of the hole is independent of the density ρ.
The speed of the liquid coming out of the hole is independent of the density ρ.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - C
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - D
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
12 Videos
Similar Questions
A cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
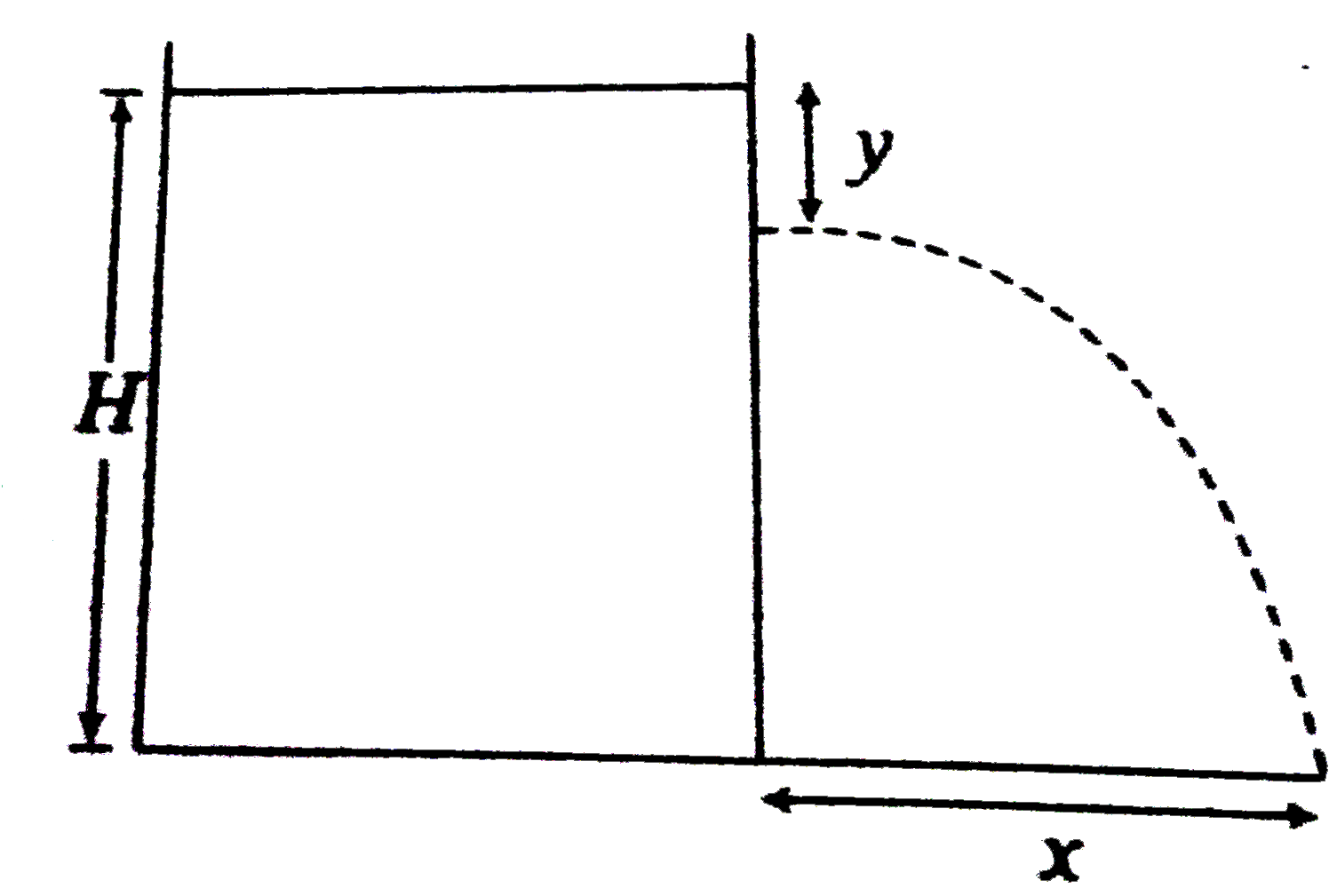
View SolutionA cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
View Solution
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depthA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
AhρgBhρ(g+a)Chρ(g−a)D2hρg(g−ag+a)A liquid is filled in a vessel and a hole is made at a depth h below the free surface of the liquid.
Statement-1 : Greater is the distance of the hole form the free surface of liquid, greater will be the velocity of efflux.
And
Statement-2 The speed of the liquid coming out of the orifice depends on the quantity of liquid in the vessel.AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1BStatement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for Statement-1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is True
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylinder is filled with non viscous liquid of density d to a hegiht h0 and a hole is made at a height h1 from the bottom of the cylinder. The velocity of liquid issuing out of the hole is
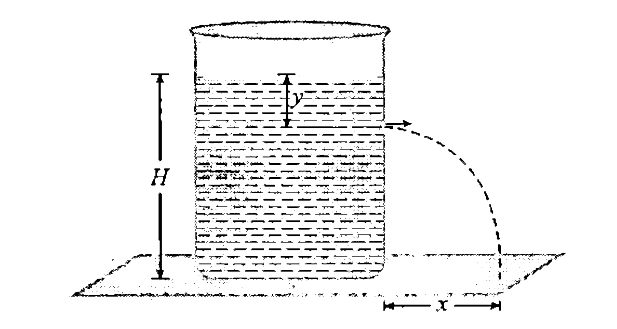
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionLiquid of density ρ in a container exerts pressure P given by (height of liquid h and area A)
View Solution