The diagonals of a parallelogram are 2ˆi and 2ˆj. What is the area of the parallelogram
0.5 unit
1 unit
1.5 unit
2 units
The correct Answer is:D
Let →Pand→Q be the sides of the parallelogram.
Them →P+→Q=2ˆiand→P−→Q=2ˆj
∴2→P=2ˆi+2ˆj or →P=ˆi+ˆj
∴ˆi+ˆj+→Q=2ˆi ∴→Q=ˆi−ˆj

Area of a parallelogram
=|P×Q|=∣∣(ˆi+ˆj)×(ˆi−ˆj)∣∣
=∣∣(−i×j)+(→j×→i)∣∣=∣∣−ˆk=ˆk∣∣=∣∣−2ˆk∣∣
∴ Area = 2 units
Topper's Solved these Questions
- VECTORSBOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - MULTIPLE CHOICE QUESTIONS (STANDARD LEVEL)
84 Videos
- VECTORSBOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - TEST YOUR GRASP
10 Videos
- REFRACTION OF LIGHT BOOK - MARVEL PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - Test Your Grasp
10 Videos
Similar Questions
Knowledge Check
Diagonals of a parallelogram PQRS must be a
ArectangleBsquareCcyclic quadrilateralDrhombusIf 3ˆi+ˆj−2ˆkandˆi−3ˆj+4ˆk are the diagonals of a parallelogram, then the area of the parallelogram is
A10√3sq.unitsB5√3sq.unitsC5√2sq.unitsD10√2sq.unitsIf the diagonals of a parallelogram are 3ˆi+ˆj−2ˆkandˆi−3ˆj+4ˆk, then the lengths of its sides are
A√8,√10B√6,√14C√5,√12Dnone of these
The given figure shows a parallelogram of 20 m height. The base of the parallelogram is 40 m long.
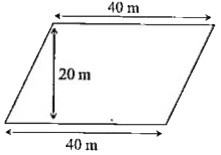
What is the area of the parallelogram?
View SolutionThe sides of a parallelogram are 2ˆi+4ˆ−5ˆkandˆi+2ˆj+3ˆk. The unit vector parallel to one of the diagonal is (A) 1√69(ˆi+2ˆj−8ˆk) (B) 1√69(−ˆi+2ˆj+8ˆk) (C) 1√69(−ˆi−2ˆj−8ˆk) (D) 1√69(ˆi+2ˆj+8ˆk)
View SolutionThe base of a parallelogram is (2x+3) units and the corresponding height is (2x–3) units. Find the area of the parallelogram in terms of x. What will be the area of parallelogram of x=30 units?
View SolutionOne of diagonal of a parallelogram is 10 cm and an angle of the parallelogram is π/4. If its height be 8 cm then area of the parallelogram :
View SolutionOne of diagonal of a parallelogram is 10 cm and an angle of the parallelogram is π/4. If its height be 8 cm then area of the parallelogram :
View Solution
