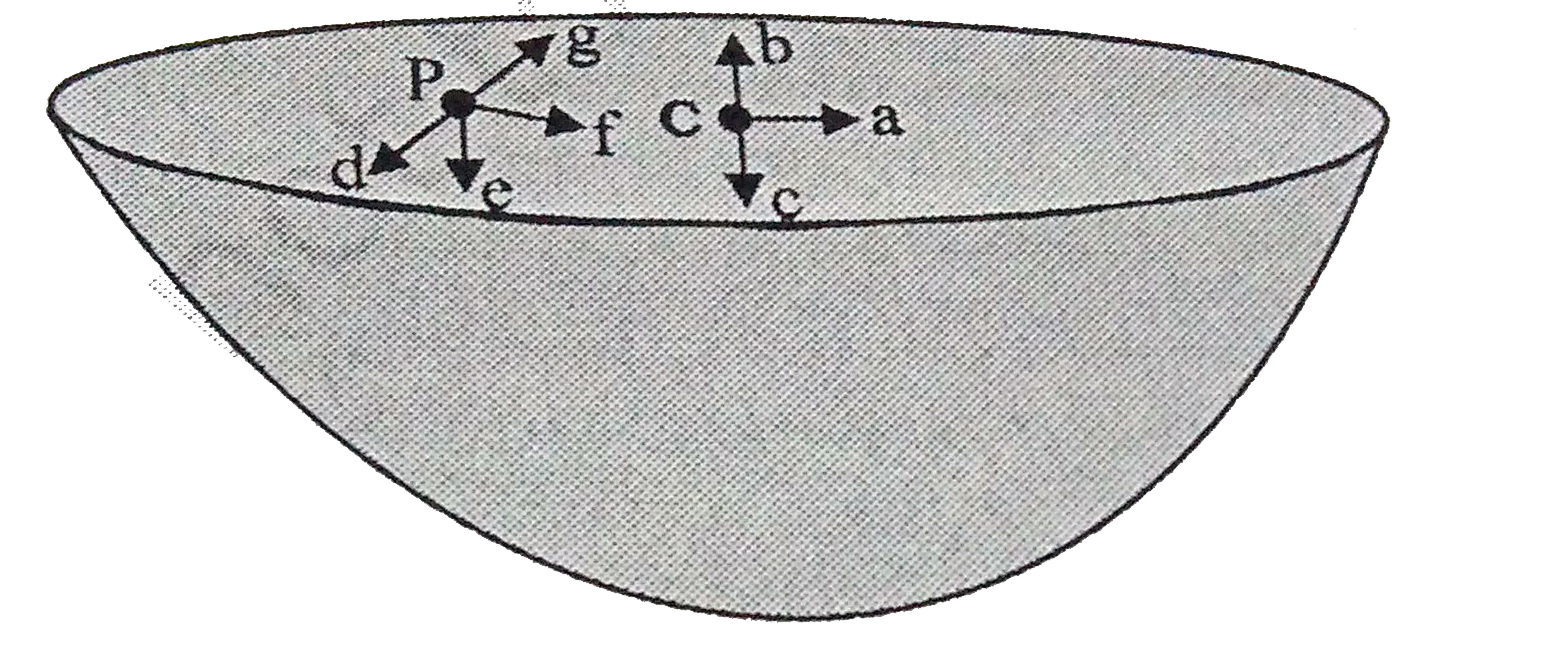
The direction of gravitational intensity at point P of a hemispherical shell of uniform mass desity is indicated by the arrow

d
e
f
g
The correct Answer is:B
(b) The direction of gravitational intensity at point P will be along e. Hence, option (b) is correct.
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Higher Order Thinking Skills
10 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - NCERT Exemplar
8 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Weightlessness
2 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
In the following two exercises, choose the correct answer from among the given ones: The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig.) (i) a, (ii) b, (iii) c, (iv) 0.
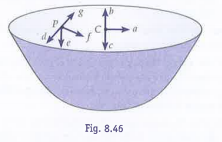
View SolutionThe gravitation intensity at the centre C of the drumhead defined by a hemispherical shell has the direction indicated by the arrow [see Fig. 8.46]
View Solution
Knowledge Check
Intensity of gravitational field inside the hollow spherical shell is
AVariableBminimumCmaximumDzeroWhat is the intensity of gravitational field of the centre of a spherical shell
AGm/r2BgCZeroDNone of theseThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3
The gravitation intensity at the centre C of the drumhead defined by a hemispherical shell has the direction indicated by the arrow [see Fig. 8.46]

View SolutionFor the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii), e, (iii) f (iv) g.
View SolutionFor the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii), e, (iii) f (iv) g.
View SolutionGravitational intensity at a point is equal to the negative of____at that point.
View SolutionThe force of attraction due to a hollow spherical shell of uniform density on a point mass situated inside is zero, so can a body be shielded from gravitational influence?
View Solution
