The disc of radius r is confined to roll without slipping at A and B. If the plates have the velocities shown, then
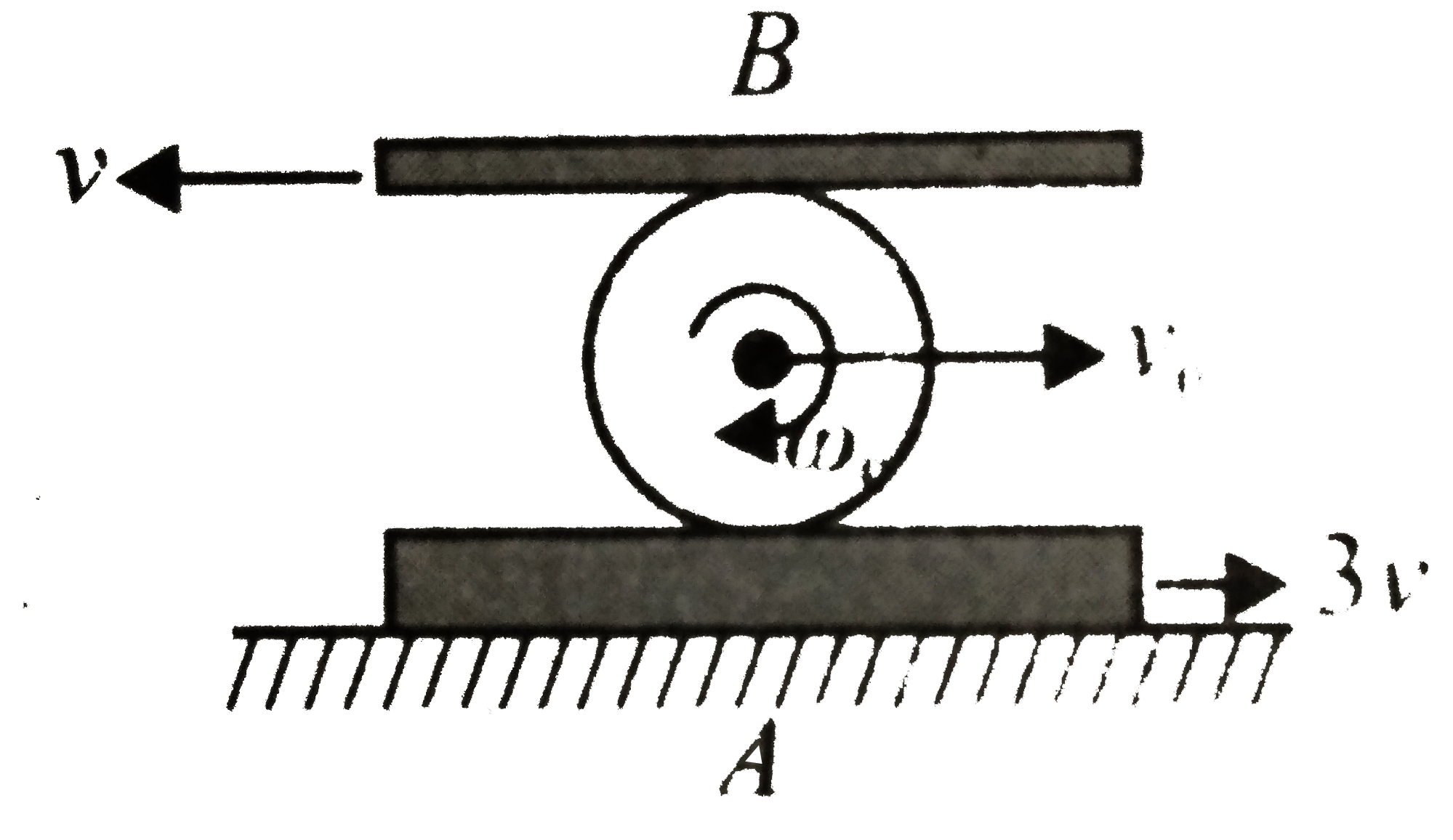
angular velocity of the disc is 2V/r
linear velocity V0=V
angular velocity of the disc is 3V/2r
none of these
The correct Answer is:A, B
v0=rω0=3v……i
v0+rω0=−v….ii
From eqn i and ii we get
2v0=2v⇒v0=v
v0+v0=−rω0⇒ω=2vr
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
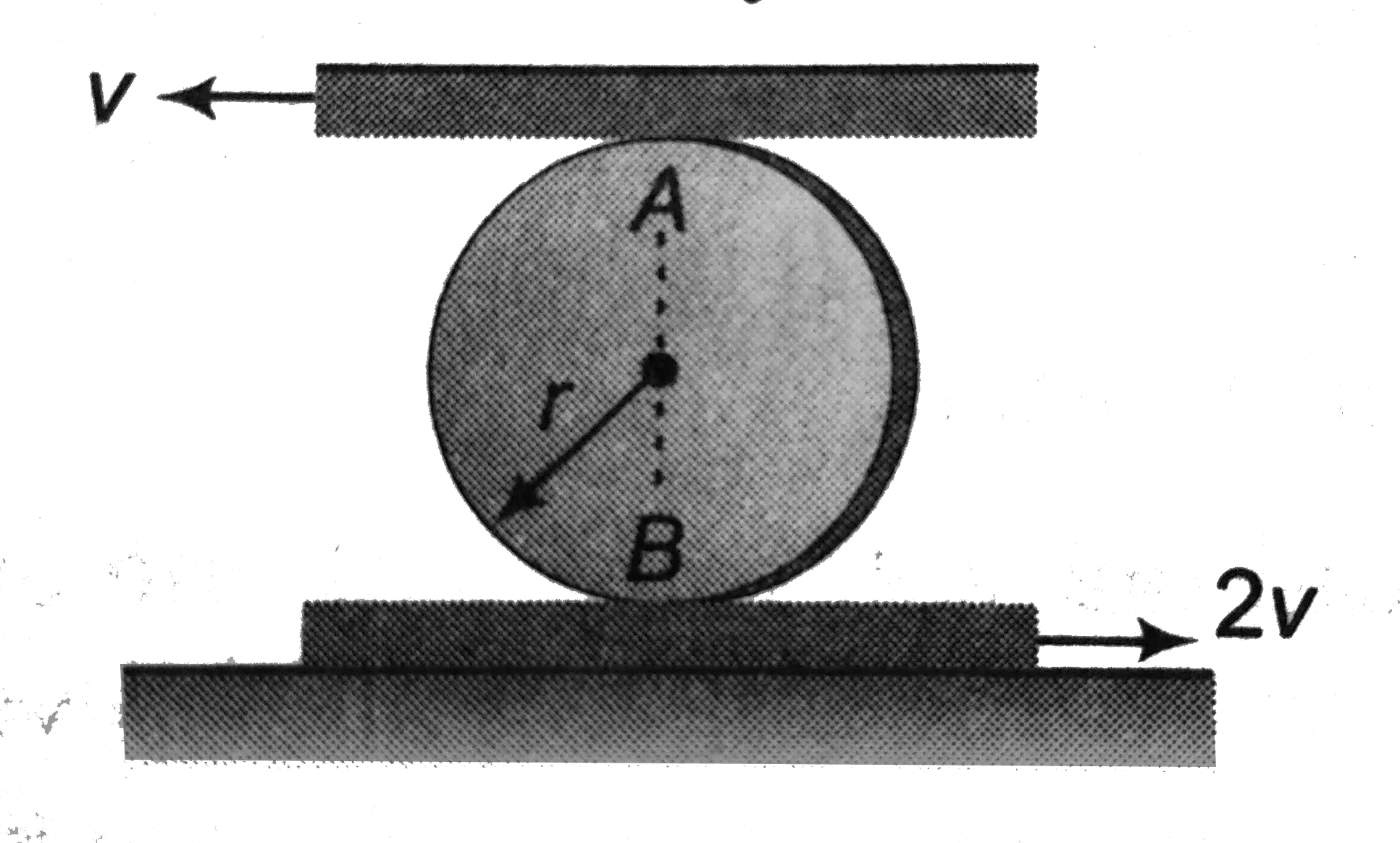
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionA circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View Solution
Knowledge Check
A disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is
 A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwise
A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwiseA disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.

Speed of point P having coordinates (x,y) isAv√x2+y2RBv√x2+(y+R)2RCv√x2−(y−R)2RDnoneA disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.
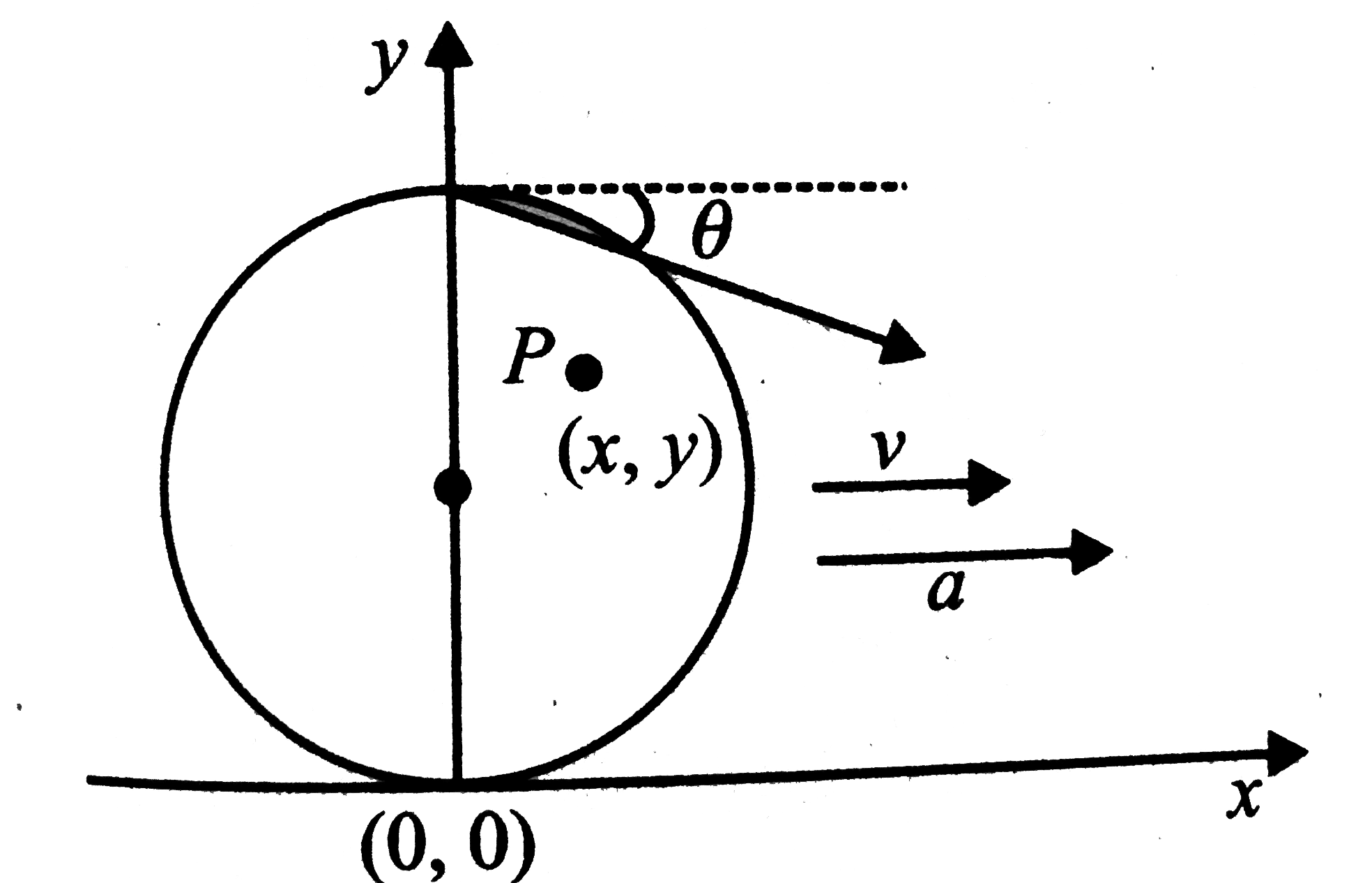
If v=√2aR the angle ρ between acceleration of the top most point and the horizontal isA0B45∘Ctan−1(2)Dtan−1(12)
A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View SolutionA disc of radius R and mass M is rolling horizontally without slipping with speed with speed v. It then moves up an incline as shown in figure. The maximum height upto which it can reach is.
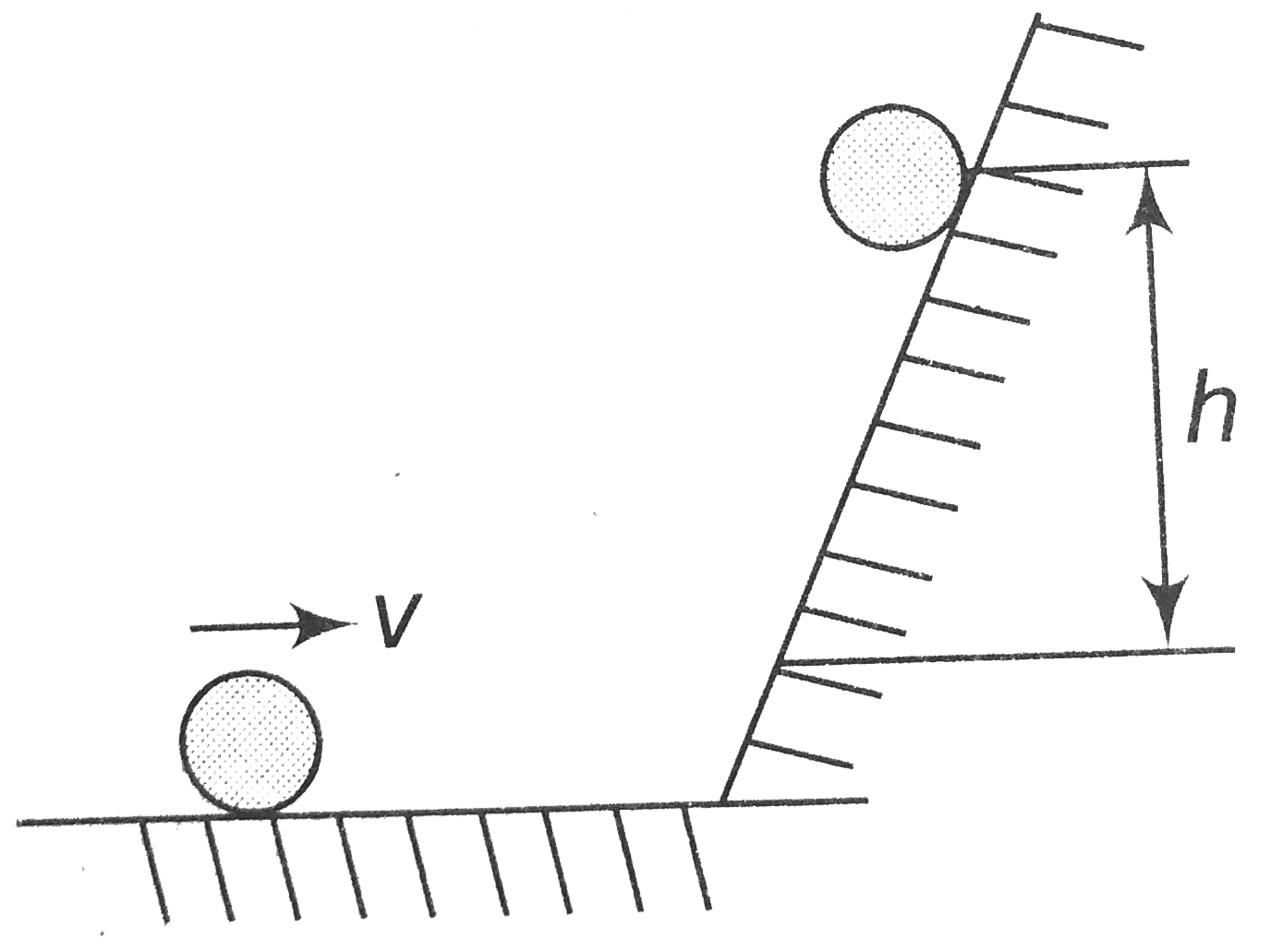 .
.
View Solution
