Two horizontal discs of different radii are free to rotate about their central vertical axes: One is given some angular velocity, the other is stationary. Their rims arc now brought in contact. There is friction between the rims. Then
the force of friction between the rims will disappear when the discs rotate with equal angular speeds
the force of friction between the rims will when they have equal linear velocities
the angular momentum of the system will conserved
the rotational kinetic energy of the system will not conserved
The correct Answer is:B, D
The force of friction between the two surface in contact disappears when there is no relative (linear) motion between them. Angular momentum will not be coserved as the discs will have the final angular velocities in the opposite directions
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Two horizontal discs A and B of radii r and 2r having moments of inertia I and 4I about their axes. Initially, disc A is rotating with ω0 and disc B is at rest. Their rims are now brought in contact. The discs first slip over each other at the contact but slipping finally ceases due to the fricition between them. Find the angular speeds of the discs after the slipping ceases. Also, find the loss in kinetic energy.
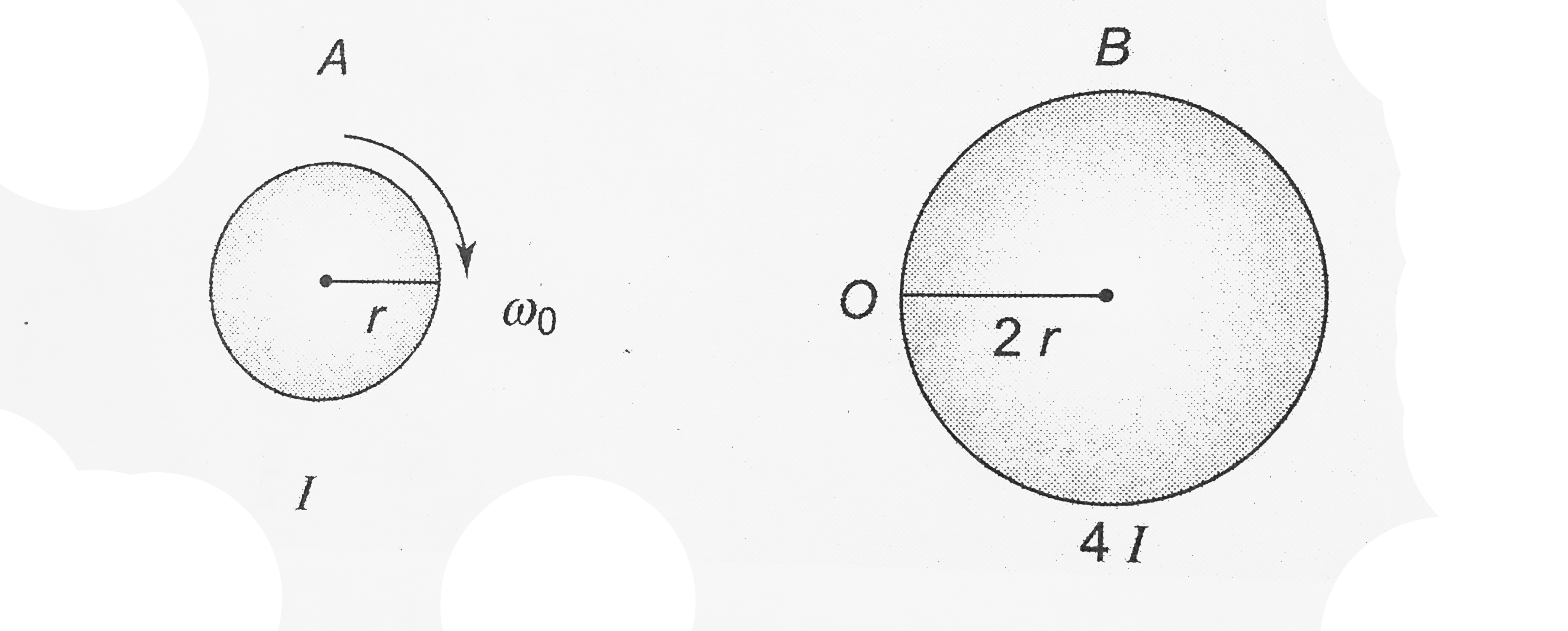
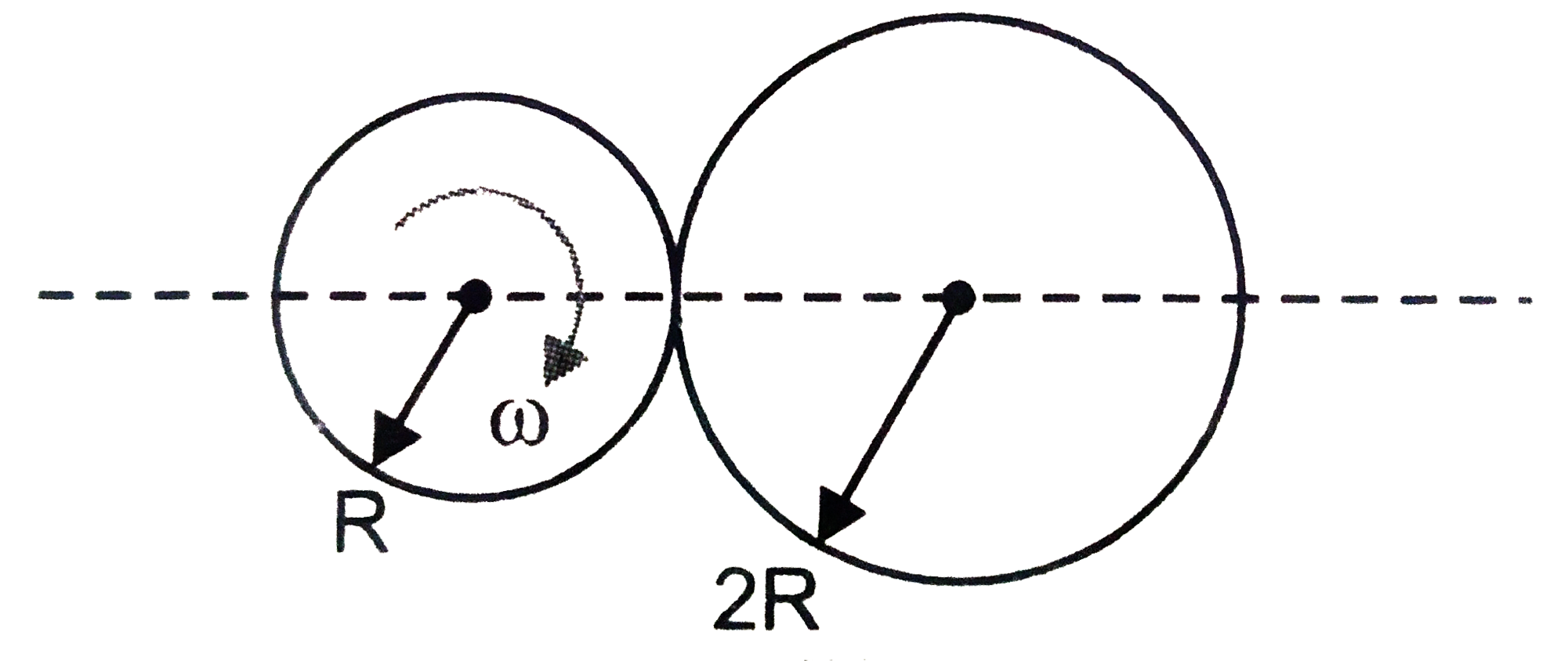
View SolutionTwo discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View Solution
Knowledge Check
Two discs of same moment of inertia rotating their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to the face coinciding the axis of rotation. The expression for loss of enregy during this process is :
A141(ω1−ω2)2B1(ω1−ω2)2C18(ω1−ω2)2D121(ω1−ω2)2Two discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2 . They are brought into contact face to face coinciding the axis of rotation . The expression for loss of energy during this process is
A14I(ω1−ω2)2BI(ω1−ω2)2C18I(ω1−ω2)2D12I(ω1+ω2)2Two men each of mass m stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass M and is free to rotate about a vertical axis passing through its centre of mass. Each man start simultaneously along the rim clockwise and reaches their original starting points on the disc. The angle turned through by the disc with respect to the ground (in radian) is:
A8mπ4m+MB2mπ4m+MCmπM+mD4mπ2M+m
A disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2rads (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without
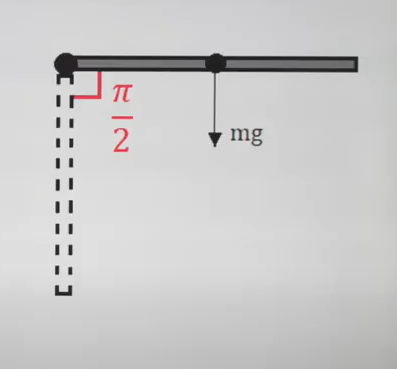
View SolutionA rod is released from the horizontal position as shown. It is free to rotate about hinge. Find angular velocity of rod when it become vertical?
View SolutionA smooth horizontal disc rotates about the vertical axis O (figure) with a constant angular velocity ω. A thin uniform rod AB of length l performs small oscillation about the vertical axis A fixed to the disc at a distance a from the axis of the disc. Find the frequency ω0 of these oscillations.

View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.

View SolutionTwo men each of mass m stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass M and is free to rotate about a vertical axis passing through its centre of mass. Each mass start simultaneously along the rim clockwise and reaches their original starting positions on the disc. The angle turned through by disc with respect to the ground (in radian) is
View Solution
