The displacement of a body is proporticonal to the cube of time elapsed. What is the nature of the acceleration of the body ?
increasing with time
decreasing with time
constant but not zero
zero
The correct Answer is:A
To solve the problem, we need to analyze the relationship between displacement, velocity, and acceleration based on the given information that the displacement of a body is proportional to the cube of time elapsed.
1. Understanding the Displacement:
- The problem states that the displacement x is proportional to the cube of time t. We can express this mathematically as:
x∝t3
- This can be rewritten as:
x=kt3
where k is a constant of proportionality.
2. Finding Velocity:
- Velocity v is defined as the rate of change of displacement with respect to time. Therefore, we differentiate x with respect to t:
v=dxdt=ddt(kt3)=3kt2
- This shows that the velocity is proportional to t2.
3. Finding Acceleration:
- Acceleration a is defined as the rate of change of velocity with respect to time. We differentiate v with respect to t:
a=dvdt=ddt(3kt2)=6kt
- This indicates that acceleration is proportional to t.
4. Analyzing the Nature of Acceleration:
- From the expression a=6kt, we see that as time t increases, the acceleration a also increases (since k is a constant).
- Therefore, we conclude that the acceleration of the body is increasing with time.
5. Final Conclusion:
- The nature of the acceleration of the body is that it is increasing with time.
- The problem states that the displacement x is proportional to the cube of time t. We can express this mathematically as:
x∝t3
- This can be rewritten as:
x=kt3
where k is a constant of proportionality.
- Velocity v is defined as the rate of change of displacement with respect to time. Therefore, we differentiate x with respect to t:
v=dxdt=ddt(kt3)=3kt2
- This shows that the velocity is proportional to t2.
- Acceleration a is defined as the rate of change of velocity with respect to time. We differentiate v with respect to t:
a=dvdt=ddt(3kt2)=6kt
- This indicates that acceleration is proportional to t.
- From the expression a=6kt, we see that as time t increases, the acceleration a also increases (since k is a constant).
- Therefore, we conclude that the acceleration of the body is increasing with time.
- The nature of the acceleration of the body is that it is increasing with time.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION
32 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - INSTANTANEOUS VELOCITY AND SPEED
16 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
The displacement of a body is given to be proportional to the cube of time elapsed. The magnitude of the acceleration of the body is
View SolutionThe acceleration of a body in SHM is
View SolutionThe position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
View SolutionThe distance covered by a moving body is directly proportional to the square to the time. The acceleration of the body is
View SolutionA variable force F acts on a body which is free to move. The displacement of the body is proportional to t3, where t = time. The power delivered by F to the body will be proportional to
View SolutionAn example of a body cube is
View SolutionThe potential energy of a body mass m is U=ax+by the magnitude of acceleration of the body will be-
View SolutionThe displacement-time graph of a body is shown in.
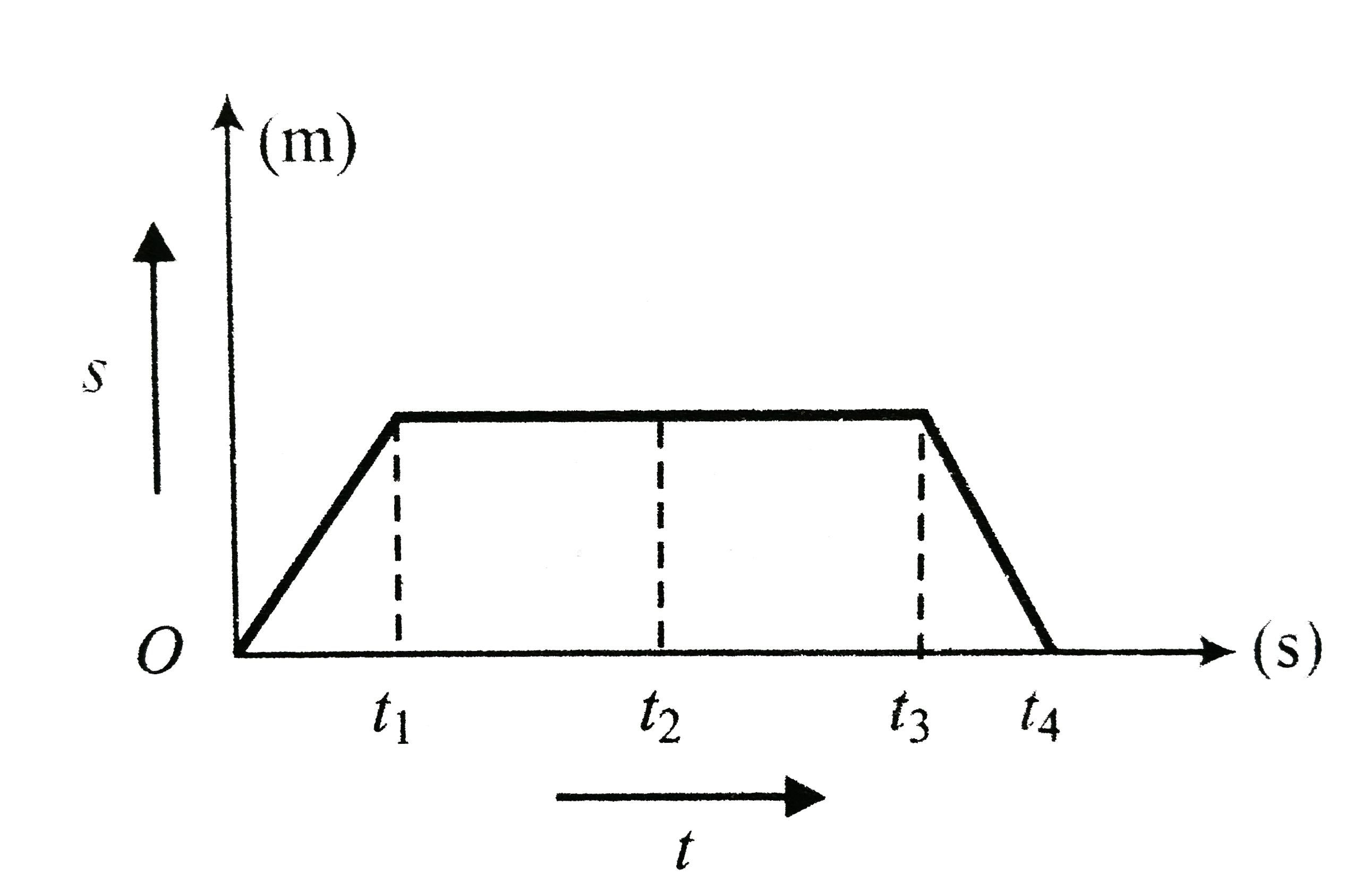 .
.
The velocity-time graph of the motion of the body will be .
View SolutionThe displacement of a body is given by s=12gt2 where g is acceleration due to gravity. The velocity of the body at any time t is
View SolutionThe velocity of a particle moving in a straight line is directly proportional to 3/4th power of time elapsed. How does its displacement and acceleration depend on time?
View Solution
