The ear ring of a lady shown in figure has a 3 cm long light suspension wire. A. Find the time period of small oscillations if the lady is standing on the ground. b. The lady now sits in a merry go round moving at 4ms−1 in a circle of radius 2 m. find the time period of small oscillation of the ear ring.

The correct Answer is:A, B, C, D
l=3cm=0.03m
T=2√lg=2π√0.039.8
=0.34second
when the lady sets on the Merry go roudn the ear rings also experience, centripetal acceleration
a=v2r=422=8ms2
Resultant Acceleration
A=√(g2+a2)
=√(100++64)
=12.8ms2
The period T=2π√(lA)
=2π√(0.0312.8)
=0.30second
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2k
A uniform ring of radius 'R' is suspended from a horizontal nail 'A' as shown. Find time period of its small oscillations.

View SolutionA uniform meter stickis suspended through a small pin hole at the 10 cm mark. Find the time period of small oscillation about the point of suspension.
View SolutionThe potential energy of a particle of mass m is given by U(x)=U0(1−coscx) where U0 and c are constants. Find the time period of small oscillations of the particle.
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
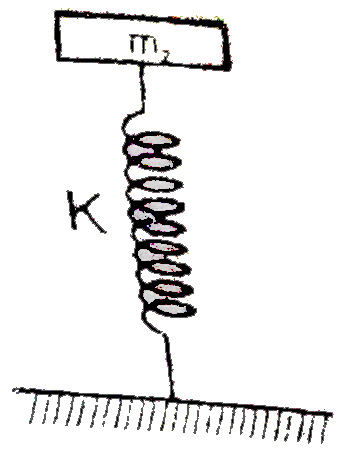
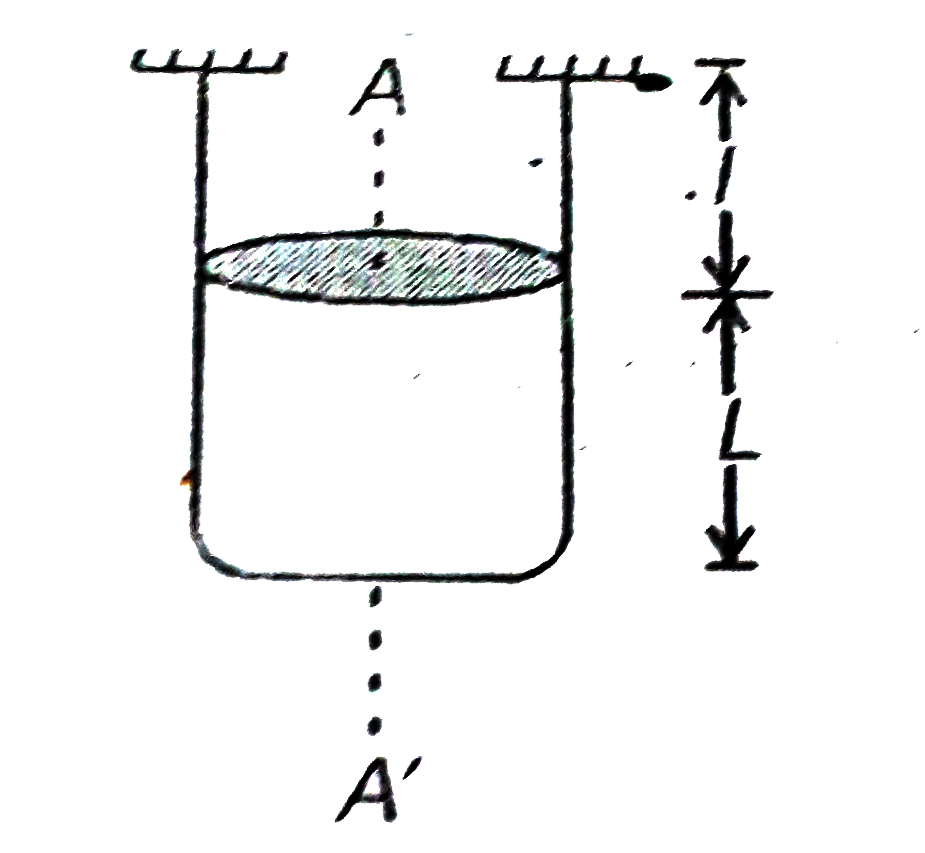
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View SolutionA square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.

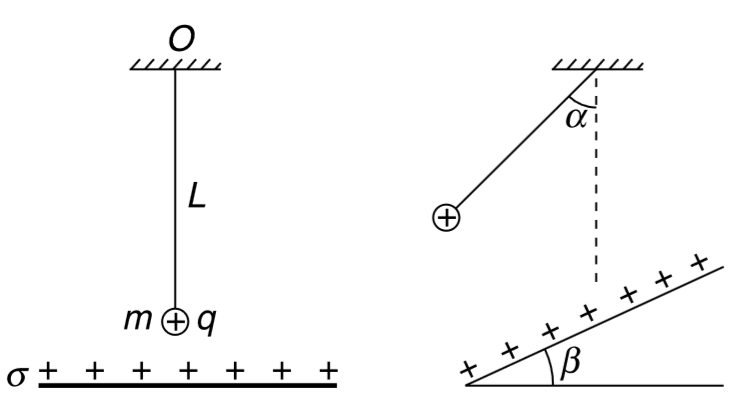
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View Solution
