The electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
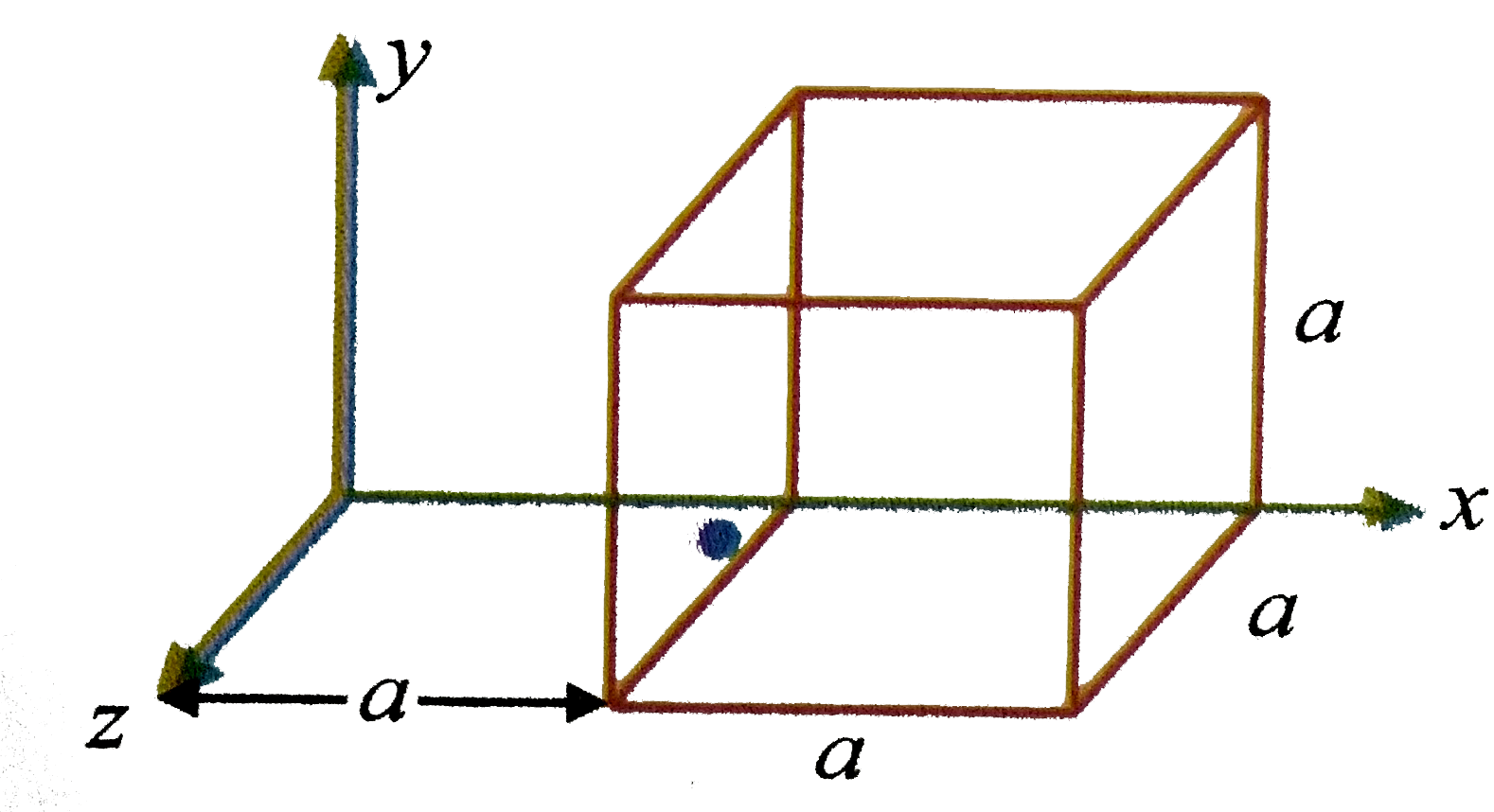
9.27×10−12C
9.27×1012C
6.97×10−12C
6.97×1012C
The correct Answer is:A
By Gauss's law, ϕ=qε0
or q=ϕε0=1.05×8.854×10−12C=9.27×10−12C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Application Of Gauss Law
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - HOTS
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Continuous Charge Distribution
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Define electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
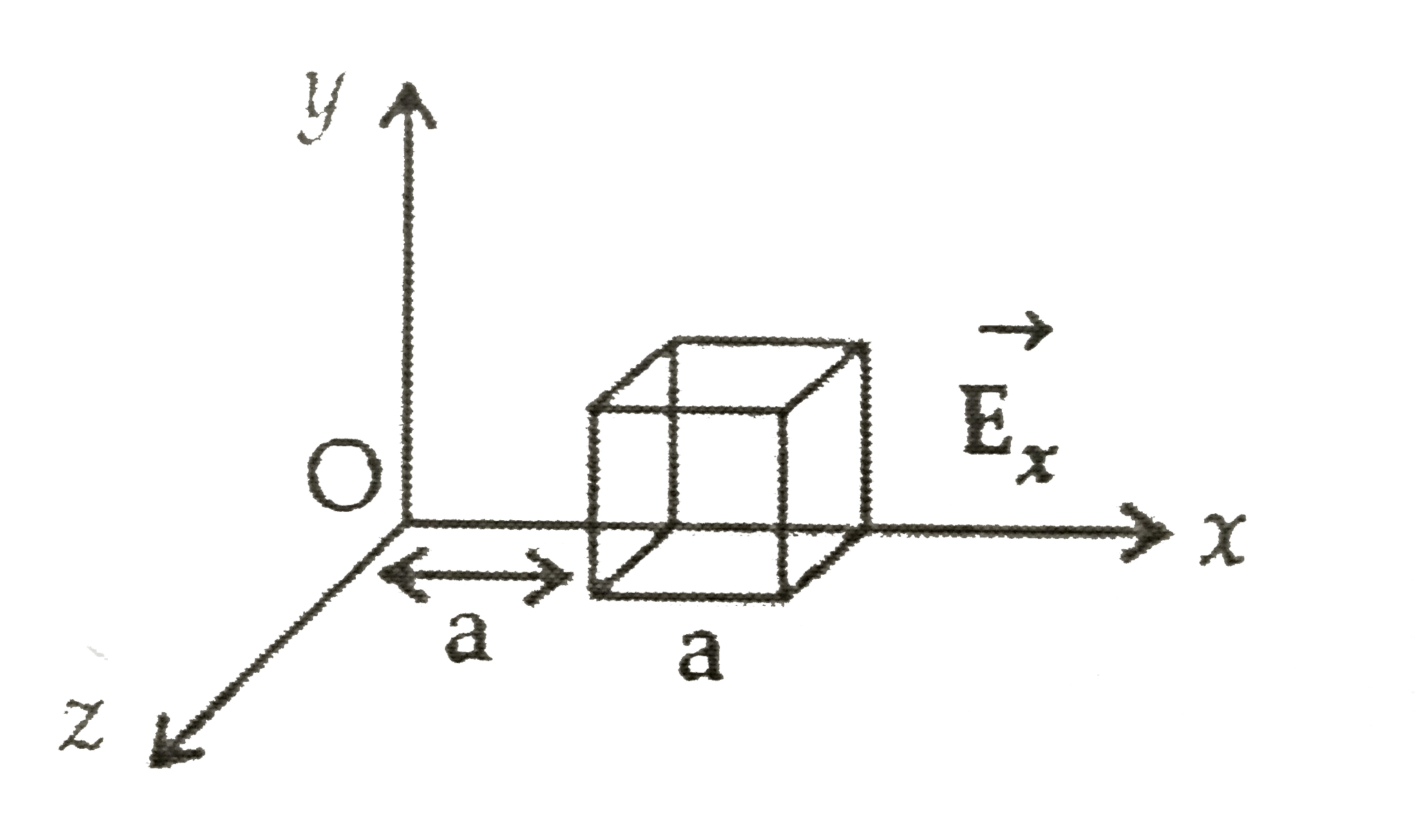
View Solution(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
View Solution
Knowledge Check
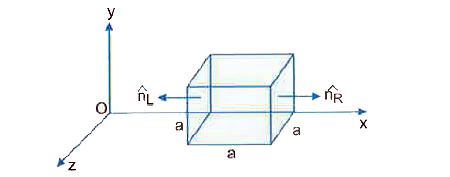
A cube of side a is placed such that the nearest face , which is parallel to the yz plane , is at a distance a from the origin . The electric field components are
Ex=αx1/2,Ey=Ez=0.
The charge within the cube is
 A√2αε0a5/2Bαε0a5/2C(√2−1)αε0a5/2Dzero
A√2αε0a5/2Bαε0a5/2C(√2−1)αε0a5/2DzeroA cube of side a is placed such that the nearest face , which is parallel to the yz plane , is at a distance a from the origin . The electric field components are
Ex=αx1/2,Ey=Ez=0.
The flux ϕE through the cube is
 A2√2αa5/2Bαa5/2C(√2−1)αa5/2Dzero
A2√2αa5/2Bαa5/2C(√2−1)αa5/2DzeroDue to a charge inside a cube the electric field is Ex=600x1/2,Ey=0,Ez=0. The charge inside the cube is (approximately):
 A600μCB60μCC7μμCD6μμC
A600μCB60μCC7μμCD6μμC
Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
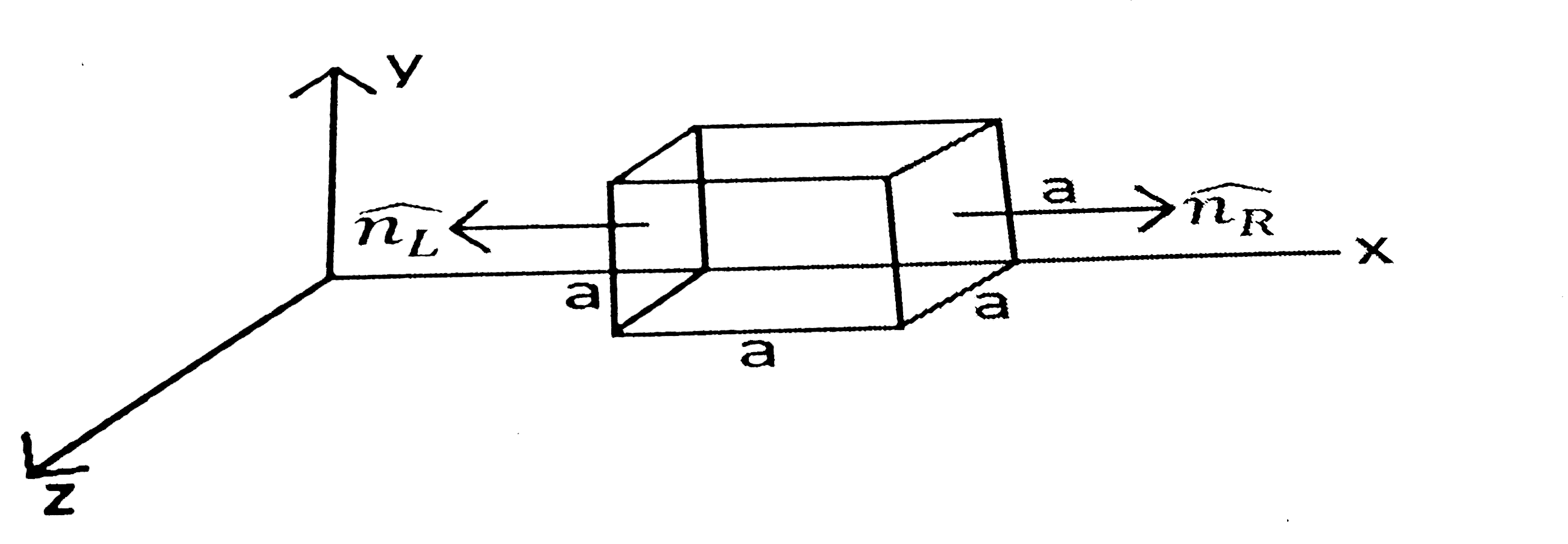
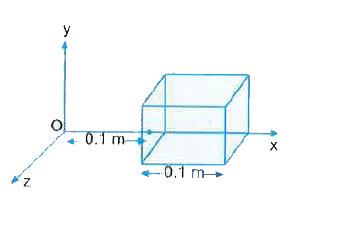
View SolutionGiven the components of an electric field as Ex=αx,Ey=0 and Ez=0, where α is a dimensional constant. Calculate the flux through each face of the cube of side a, as shown in the figure.

View SolutionThe electric field componets due to a charge inside the cube of side 0.1m are Ex=αx, where α=500(N/C)m−1,
Ey=0,Ez=0. Calculate the flux through the cube and the charge inside the cube.
View Solution(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
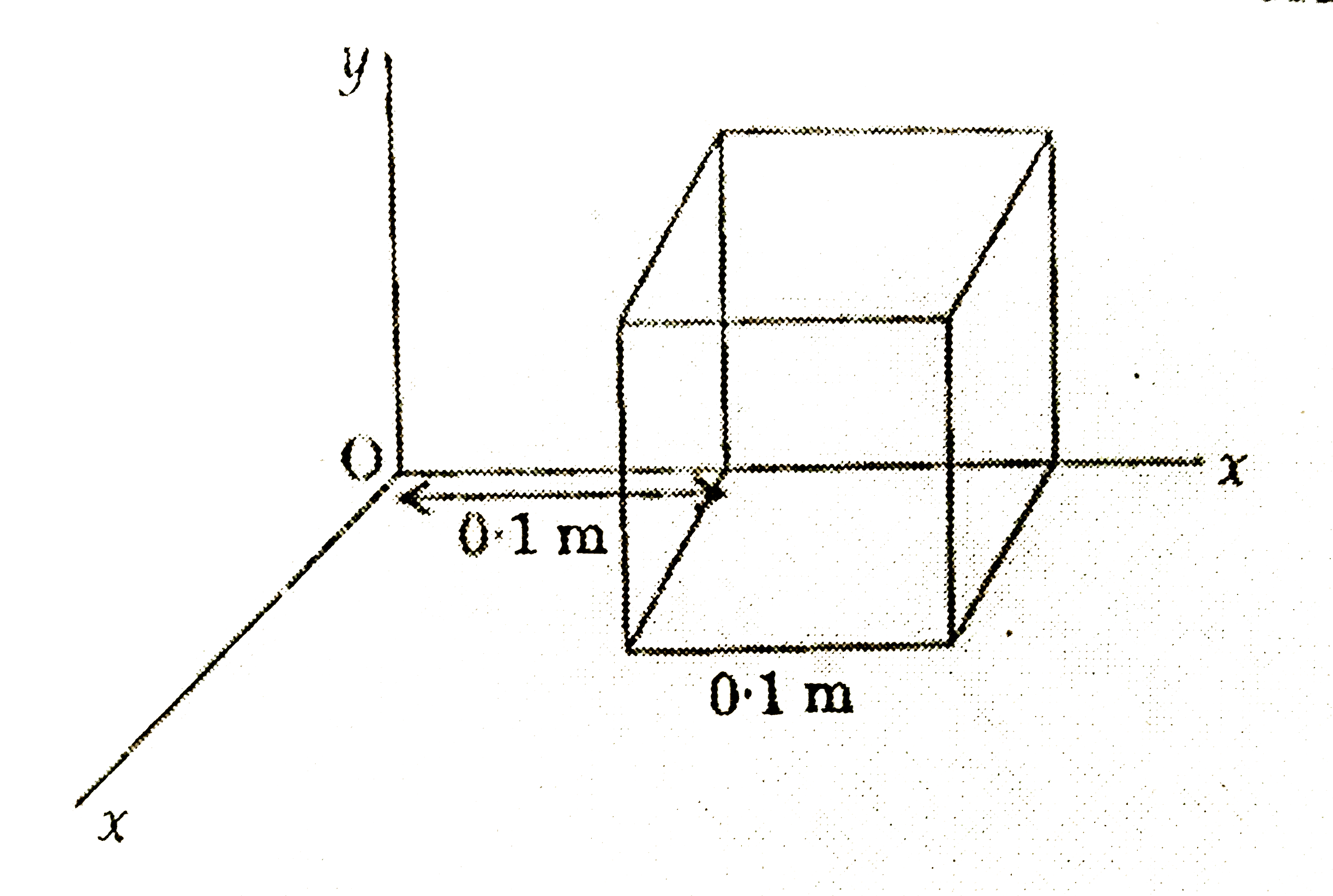
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.
View SolutionDefine electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1m area as shown in Ex=αx, where α=500N/Cm,EY=0andEZ=0.
Calculate (i) the flux through the cube , and
(ii) the charges inside the cube.
View Solution
