The electric potential decreases unifromly from 120 V to 80 V as one moves on the x-axis from x=-1 cm to x=+1 cm. The electric field at the origin
must be equal to 20Vcm−1
must be equal to 20Vm−1
may be greater than 20Vm−1
may be less than 20Vcm−1
The correct Answer is:c
To solve the problem, we need to find the electric field at the origin given that the electric potential decreases uniformly from 120 V to 80 V as we move along the x-axis from x = -1 cm to x = +1 cm.
1. Understanding the Problem:
- We know that the electric potential V decreases from 120 V to 80 V as we move from x=−1 cm to x=+1 cm.
- This indicates that there is a uniform electric field acting along the x-axis.
2. Finding the Change in Potential:
- The change in potential ΔV can be calculated as:
ΔV=Vfinal−Vinitial=80V−120V=−40V
3. Calculating the Distance:
- The distance d over which this change occurs is:
d=xfinal−xinitial=1cm−(−1cm)=2cm=0.02m
4. Using the Relationship Between Electric Field and Potential:
- The relationship between electric field E and potential difference ΔV is given by:
ΔV=−E⋅d
- Rearranging this gives:
E=−ΔVd
5. Substituting Values:
- Substituting the values we found:
E=−−40V0.02m=40V0.02m=2000V/m
6. Direction of the Electric Field:
- Since the potential decreases in the positive x-direction, the electric field must point in the direction of decreasing potential, which is towards the left (negative x-direction).
- Therefore, the electric field at the origin is:
E=−2000V/m(in the negative x-direction)
Final Answer:
The electric field at the origin is 2000V/m directed towards the negative x-axis.
- We know that the electric potential V decreases from 120 V to 80 V as we move from x=−1 cm to x=+1 cm.
- This indicates that there is a uniform electric field acting along the x-axis.
- The change in potential ΔV can be calculated as:
ΔV=Vfinal−Vinitial=80V−120V=−40V
- The distance d over which this change occurs is:
d=xfinal−xinitial=1cm−(−1cm)=2cm=0.02m
- The relationship between electric field E and potential difference ΔV is given by:
ΔV=−E⋅d
- Rearranging this gives:
E=−ΔVd
- Substituting the values we found:
E=−−40V0.02m=40V0.02m=2000V/m
- Since the potential decreases in the positive x-direction, the electric field must point in the direction of decreasing potential, which is towards the left (negative x-direction).
- Therefore, the electric field at the origin is:
E=−2000V/m(in the negative x-direction)
The electric field at the origin is 2000V/m directed towards the negative x-axis.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
The electric potential decreases uniformly from 180V to 20V as one moves on the X-axis from x=−2cm to x=+2cm. The electric field at the origin:
View SolutionThe electric potential decreases uniformly from 100V to 50V as one moves along the x-axis from x=0 to x=5m. The electric field at x=2m must be equal to 10V/m. Is this statement true or false.
View SolutionIf on the x - axis electric potential decreases uniform from 60 V to 20 V between x = -2 m to x = +2 m then the magnitude of electric field at the origin
View SolutionThe electric potential decreases uniformly from V to -V along X-axis in a coordinate system as we moves from a point (−x0,0) to (x0,0), then the electric field at the origin:
View SolutionThe electric potential V at any point (x,y,z), all in meters in space is given by V=4x2 volt. The electric field at the point (1,0,2) in volt//meter is
View SolutionThe electric potential V at any point x, y, z (all in meters) in space is given by V=4x2 volts. The electric field at the point (1m, 0, 2m) is……………..V/m.
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by V=4x2 volt. The electric field at the point (1m,0,2m) is ……………Vm.
View SolutionThe figure gives the electric potential V as a function of distance through five regions on x-axis. Which of the following is true for the electric E in these regions ?
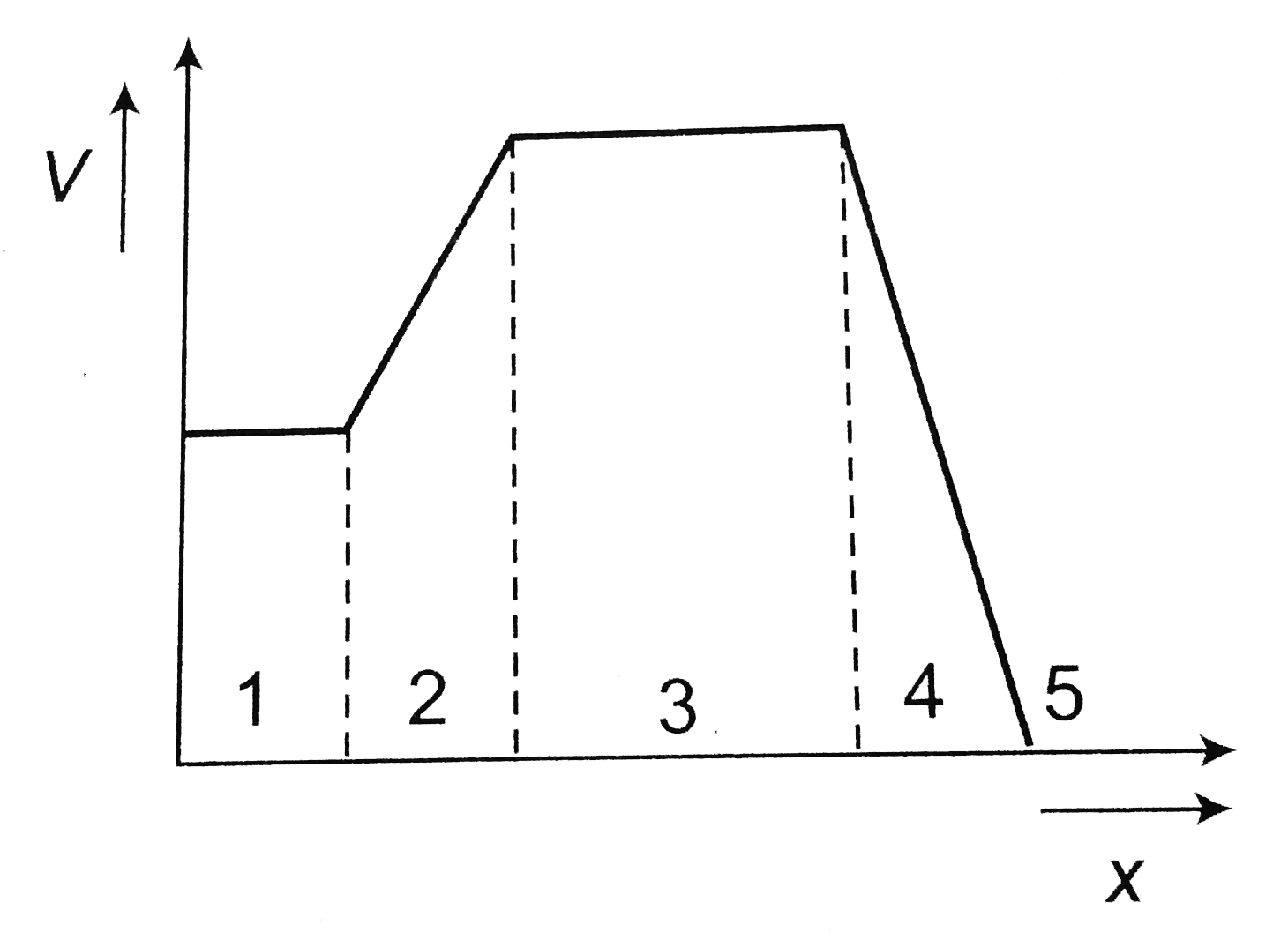
View SolutionThe electric potential V is givne as a function of distance x (metre) by V=(5x2+10x−9) volt. Value of electric field at x=1is
View SolutionThe electric potential V is givne as a function of distance x (metre) by V=(5x2+10x−9) volt. Value of electric field at x=1is
View Solution
