The electric potential V is givne as a function of distance x (metre) by V=(5x2+10x−9) volt. Value of electric field at x=1is
−20Vm−1
6Vm−1
11Vm−1
−23Vm−1
The correct Answer is:A
To find the electric field E at x=1 meter given the electric potential V as a function of distance x, we can follow these steps:
Step 1: Write down the expression for electric potential
The electric potential V is given by:
V=5x2+10x−9
Step 2: Calculate the electric field
The electric field E is related to the electric potential V by the formula:
E=−dVdx
Thus, we need to differentiate V with respect to x.
Step 3: Differentiate the potential function
We differentiate V:
dVdx=ddx(5x2+10x−9)
Using the power rule of differentiation:
dVdx=10x+10
Step 4: Substitute x=1 into the derivative
Now we substitute x=1 into the expression for dVdx:
dVdx∣∣∣x=1=10(1)+10=10+10=20
Step 5: Calculate the electric field
Now, substituting this result back into the equation for the electric field:
E=−dVdx=−20V/m
Final Answer
The value of the electric field at x=1 meter is:
E=−20V/m
---
The electric potential V is given by:
V=5x2+10x−9
The electric field E is related to the electric potential V by the formula:
E=−dVdx
Thus, we need to differentiate V with respect to x.
We differentiate V:
dVdx=ddx(5x2+10x−9)
Using the power rule of differentiation:
dVdx=10x+10
Now we substitute x=1 into the expression for dVdx:
dVdx∣∣∣x=1=10(1)+10=10+10=20
Now, substituting this result back into the equation for the electric field:
E=−dVdx=−20V/m
The value of the electric field at x=1 meter is:
E=−20V/m
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.3
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
The electric potential V is given as a function of distance x (metre) by V=(6x2+10x−9) volt. Find magnitude of electric field (in V/m) at x= 4.
View SolutionThe electric potential V at any point (x,y,z), all in meters in space is given by V=4x2 volt. The electric field at the point (1,0,2) in volt//meter is
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by V=4x2 volt. The electric field at the point (1m,0,2m) is ……………Vm.
View SolutionThe electric potential V at any point x, y, z (all in meters) in space is given by V=4x2 volts. The electric field at the point (1m, 0, 2m) is……………..V/m.
View SolutionElectric potential V in space as a function of cartesian co-ordinates is given by V=1x+1y+1z. Then find electric field intensity at (1, 1, 1)
View SolutionIf the potential function is define as V=(−3x+4y+12z)V, then magnitude of electric field E(x,y,z) is
View SolutionThe electric potential decreases uniformly from 100V to 50V as one moves along the x-axis from x=0 to x=5m. The electric field at x=2m must be equal to 10V/m. Is this statement true or false.
View SolutionThe figure gives the electric potential V as a function of distance through five regions on x-axis. Which of the following is true for the electric E in these regions ?
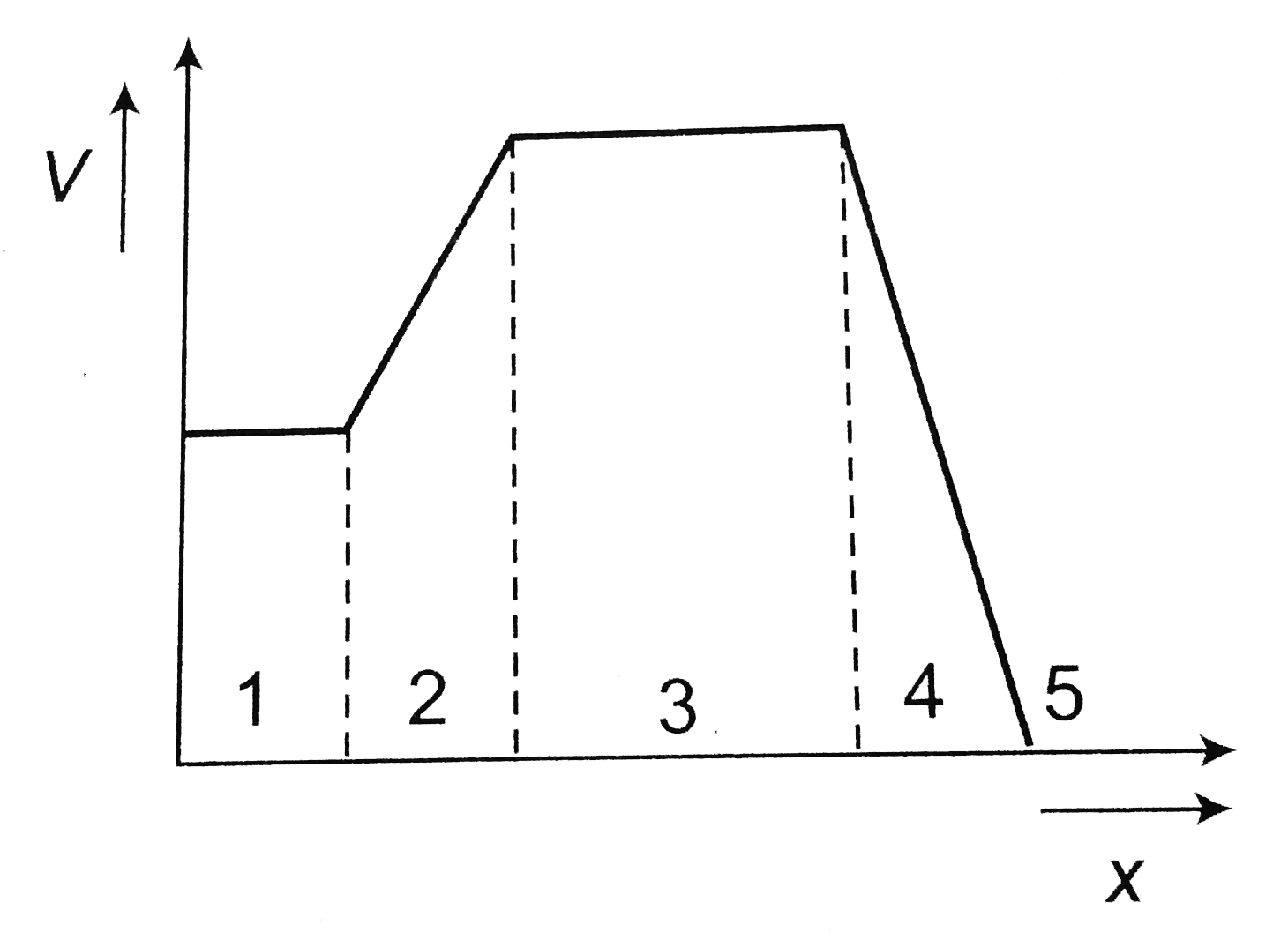
View SolutionThe electric potential at a point (x,0,0) is given by V=[1000x+1500x2+500x3] "then the electric field at" x=1 m is (in volt//m)
View SolutionIf on the x - axis electric potential decreases uniform from 60 V to 20 V between x = -2 m to x = +2 m then the magnitude of electric field at the origin
View Solution
