The ends A and B of a eod of length l have velocities of magnitudes |→vA|=v and |→vB|=2v respectively. If the inclination of →vA relationn to the rod is α find the
a. Inclination β of →cB relative of the rod.
b. angular velocity of the rod.
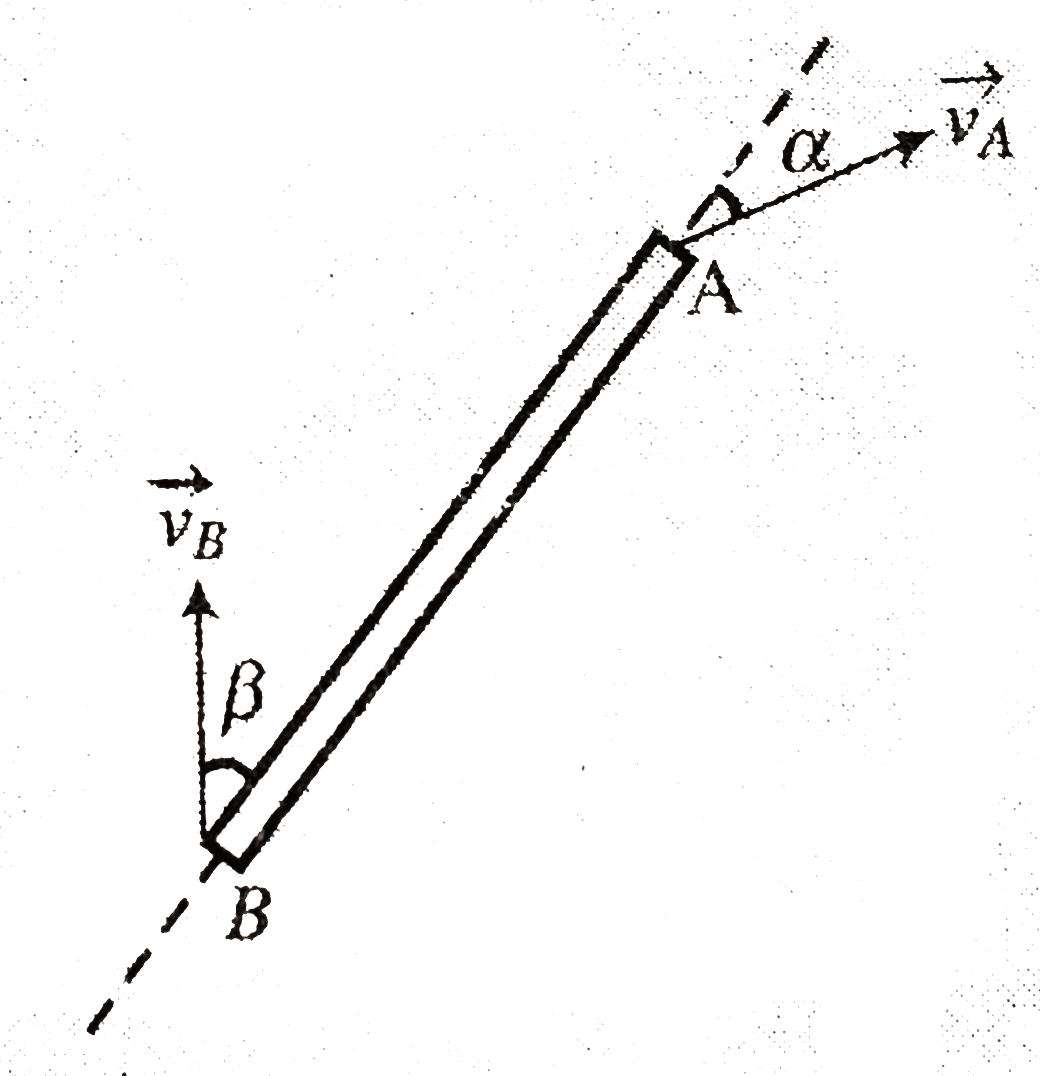
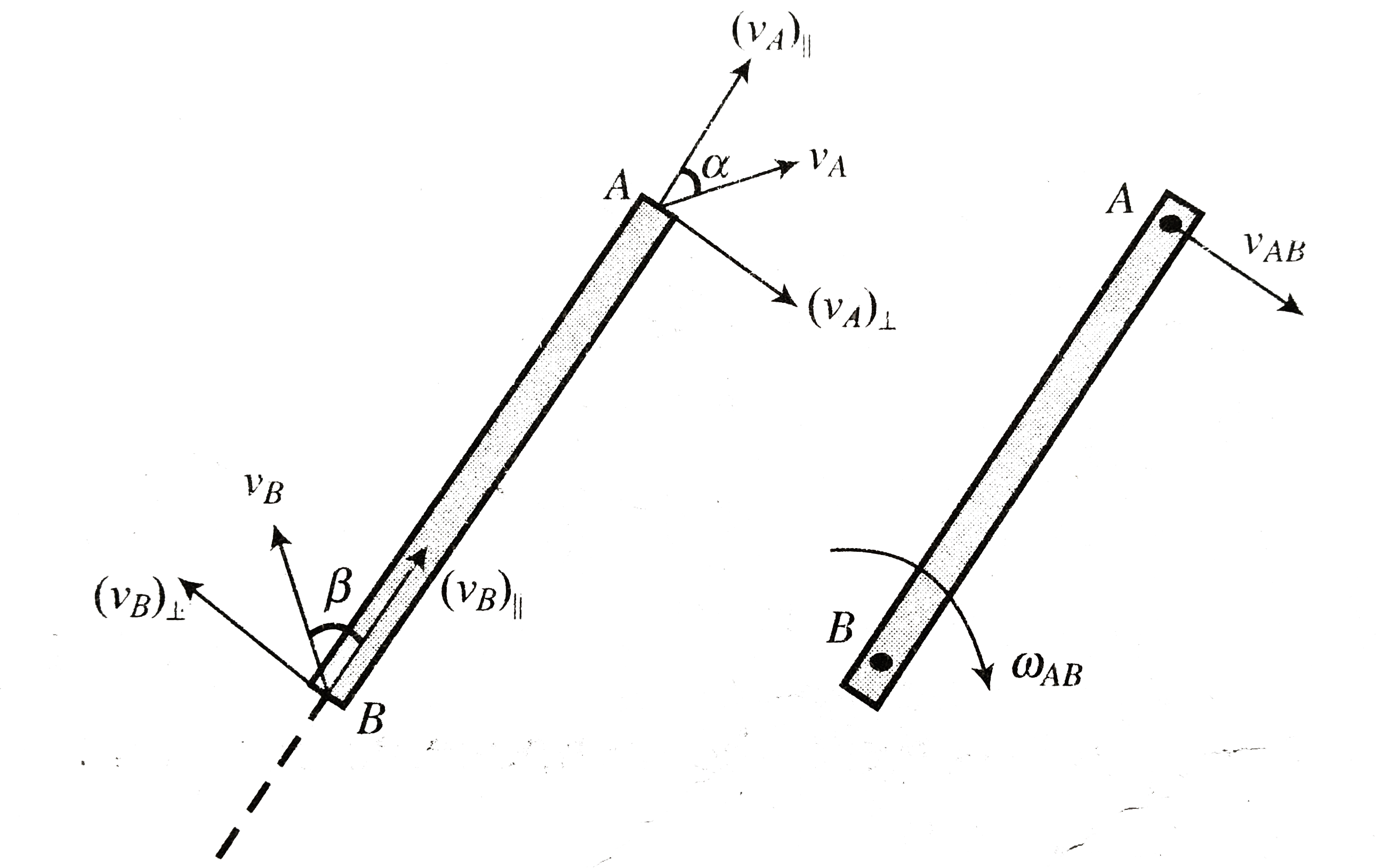
We know in a rigid body the velocities of two points along the line joining two should remain same.
i.e., (vA)∣∣=(vB)∣∣
Hence vcosθ=2vcosβ
cosβ=12cosα or β=cos−2(12cosα)
b. for angular velocity of the rod we can write
ω=∣∣(→vAB)⊥∣∣l=∣∣(→vA−→vB)⊥∣∣l
|→vAB|=|→vA−→–––(B)|=vsinα(−2vsinβ)=v(sinα+2sinβ)
⇒ω=(sinα+2sinβ)vl (in clockwise direction)
we have calculated cosβ=cosα2. Thus,
sinβ=√1−cos2β⇒sinβ=√3+sin2α2
Hence ω=sinα+√3+sinαl ( in clockwise direction)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution
Knowledge Check
In the figure shown the instantaneous speed of end A of the rod is v to the left the angular velocity of the rod of lengthL must be
 Av/2LBv/LCv√3/2LDnone
Av/2LBv/LCv√3/2LDnoneIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 Av2LBvLCv√32LDnone of these
Av2LBvLCv√32LDnone of theseThe velociies of A and B are →vA=2ˆi+4ˆjand→vB=3ˆi−7ˆj , velocity of B as observed by A is
A5ˆi−3ˆjBˆi−11ˆjC−ˆi+11ˆjD2ˆi−3ˆj
Find the instantneous axis of rotation of a rod length l when its end A moves with a velocity →vA=ˆi and the rod rotates with an angular velocity →ω=−v2lˆk.
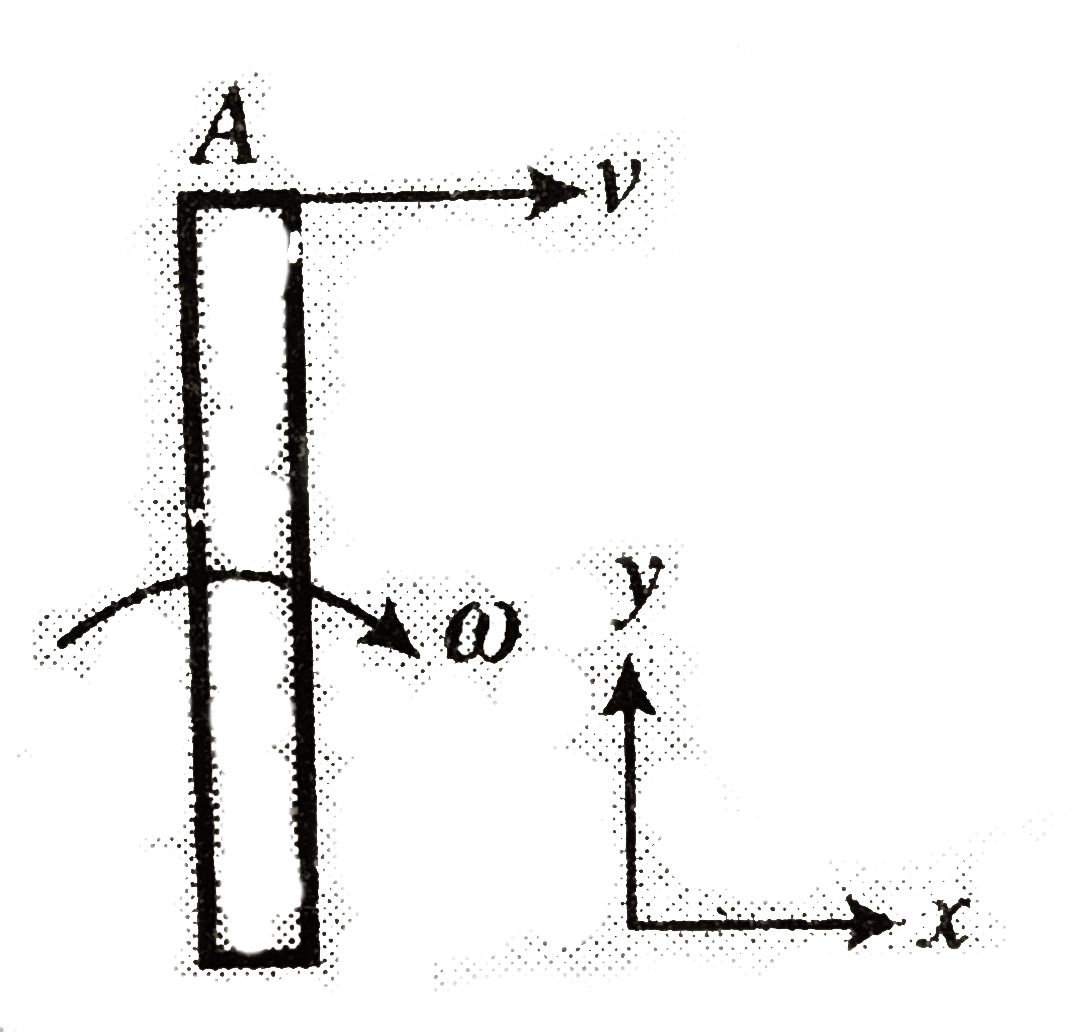
View SolutionThere is rod of length l. The velocities of its two ends are v1andv2 is opposite directions normal to the rod. The distance of the instantaneous axis of rotation from v1 is :
View SolutionSuppose that two objects A and B are moving with velocities →vA and →vB (each with respect to some common frame of refrence). Let →vAB represent the velocity of A with respect to B. Then
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionA rod AB of length 2m moves in horizontal x−y plane. At any instant end a of the rod is at origin and has velocity →vA=2ˆi+vyˆj. The other end B at the same instant is moving with velocity →vB=3ˆi+6ˆj. The rod makes an angle of 30∘ with the x−axis at this instant (see figure)
The magnitude of angular velocity of the rod is

View Solution
