Find the instantneous axis of rotation of a rod length l when its end A moves with a velocity →vA=ˆi and the rod rotates with an angular velocity →ω=−v2lˆk.
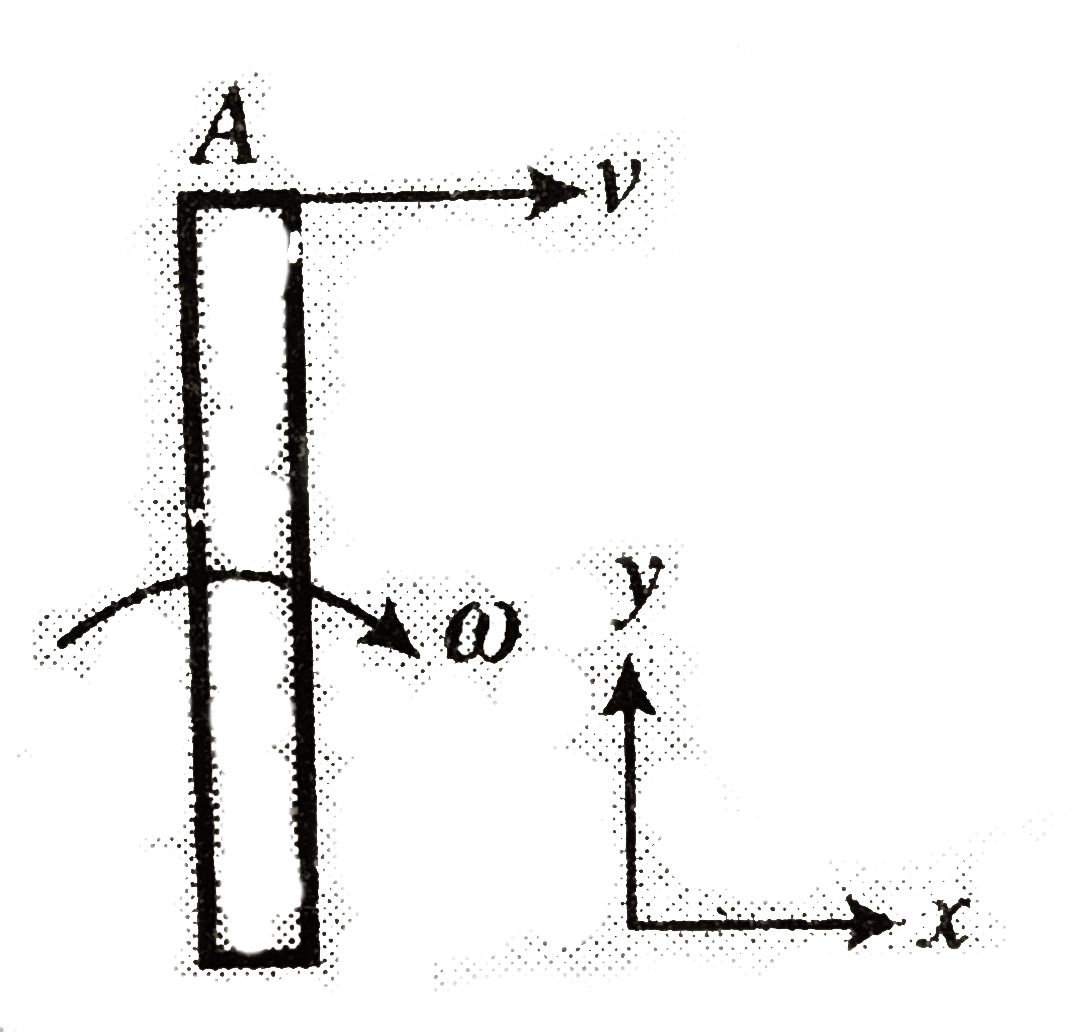
Let us choose the point P as ICR in the extended rod. We can say ICR is a point of zero velocity. So we can write
→vP=→vP,A+→vA
we have →vP=0
Hence →vP,A=→vA=0
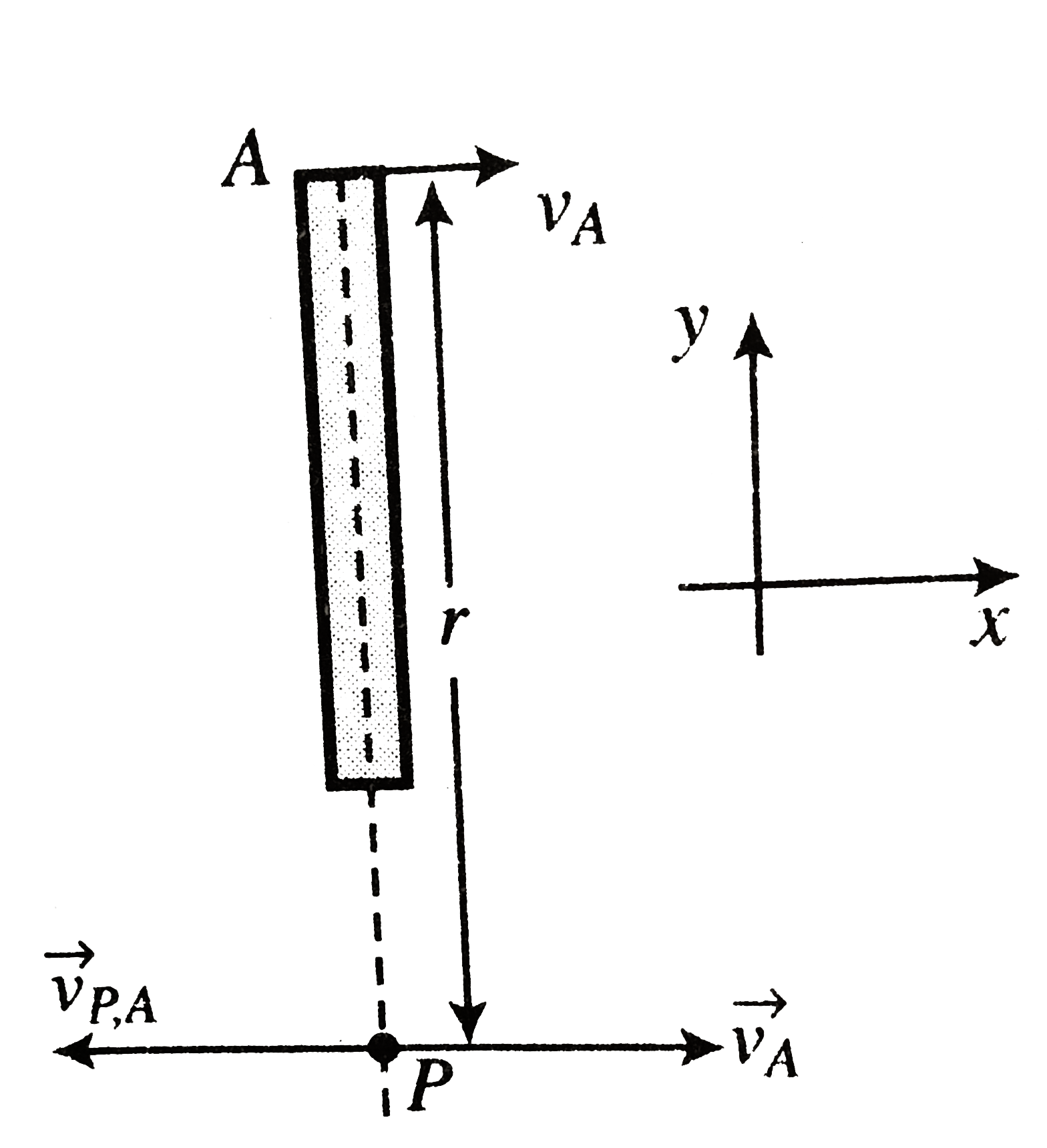
Here →–––(A)=vˆi and →vP,A=−ωˆi
Hence −ωrˆi+vˆi=0
⇒v=ωr
or r=vω=v(v2l)=2l
Hence ICR will be located at a distance 2l from A.
Method 2
The instantaneous centre of rotation will be lie on the perpendicular line at point A with →vA.
The ICR will lie at distance AP+|→vA|ω=vv2l=2l
or at a distance 2l from point A.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
If the rod were translating as well as rotating, what will be its emf? Assume that the centre of mass has a velocity v and the rod is rotating with an angular velocity ω atout its centre of mass.
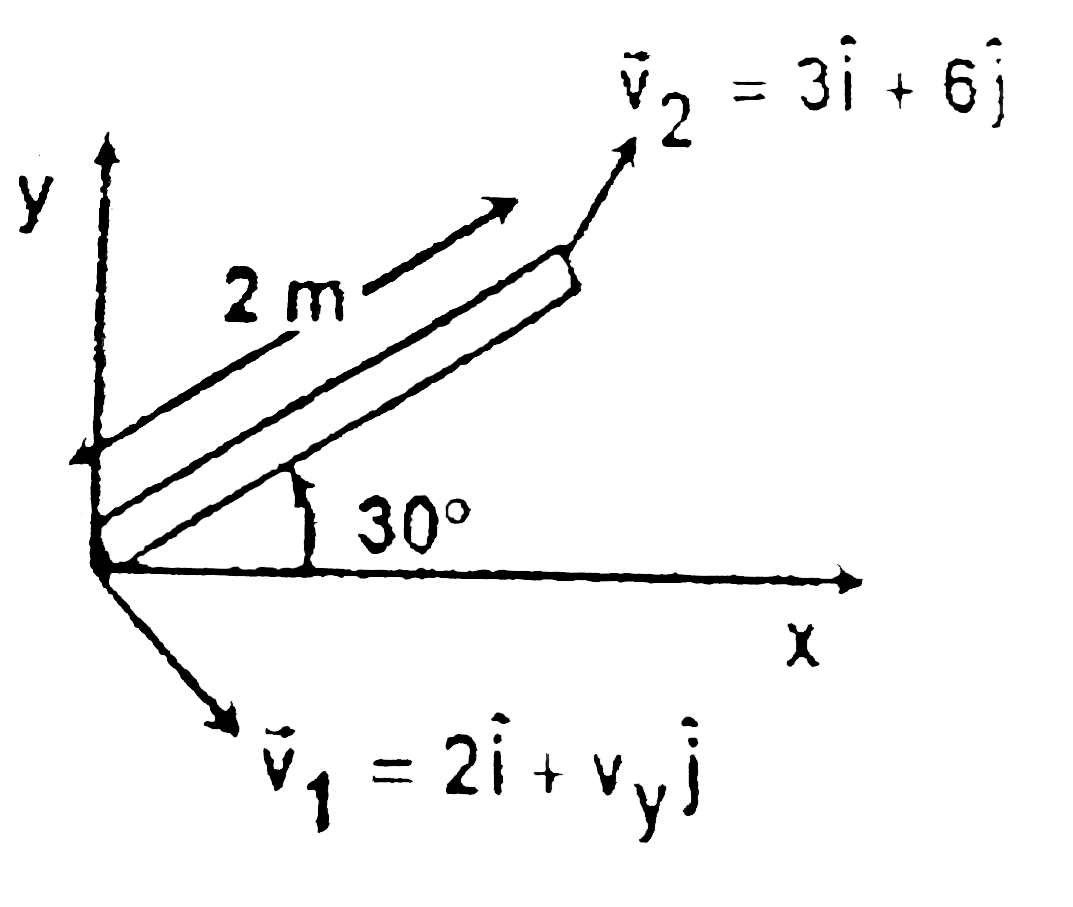
View SolutionA rod AB of length 2m moves in horizontal x−y plane. At any instant end a of the rod is at origin and has velocity →vA=2ˆi+vyˆj. The other end B at the same instant is moving with velocity →vB=3ˆi+6ˆj. The rod makes an angle of 30∘ with the x−axis at this instant (see figure)
The value of vy is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2 - Question 2 - Select One
A uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
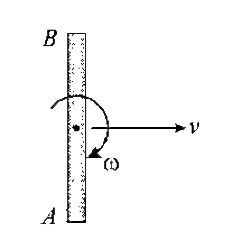 A34ωBω3Cω2D23ω
A34ωBω3Cω2D23ω - Question 3 - Select One
A rod AB of length 2m moves in horizontal x−y plane. At any instant end a of the rod is at origin and has velocity →vA=2ˆi+vyˆj. The other end B at the same instant is moving with velocity →vB=3ˆi+6ˆj. The rod makes an angle of 30∘ with the x−axis at this instant (see figure)
The magnitude of angular velocity of the rod is
 A1rad/secB√3rad/secC√32rad/secD1/2rad/sec
A1rad/secB√3rad/secC√32rad/secD1/2rad/sec
Find the value of ∣∣→V∣∣ if the linear velocity of a rotating body is given by →v=→ω×→r, where →ω is the angular velocity and →r is the radius vector. The angular velocity of a body is
→ω=ˆi−2ˆj and the radius vector
→r=2ˆj−3ˆk.View SolutionA conducting rod of length 1 is moving on a horizontal smooth surface. Magnetic field in the region is vertically downward and magnitude B0. If centre of mass (COM) of the rod is translating with velocity v0 and rod rotates about COM with angular velocity v0/l, then potential difference between points O and A will be
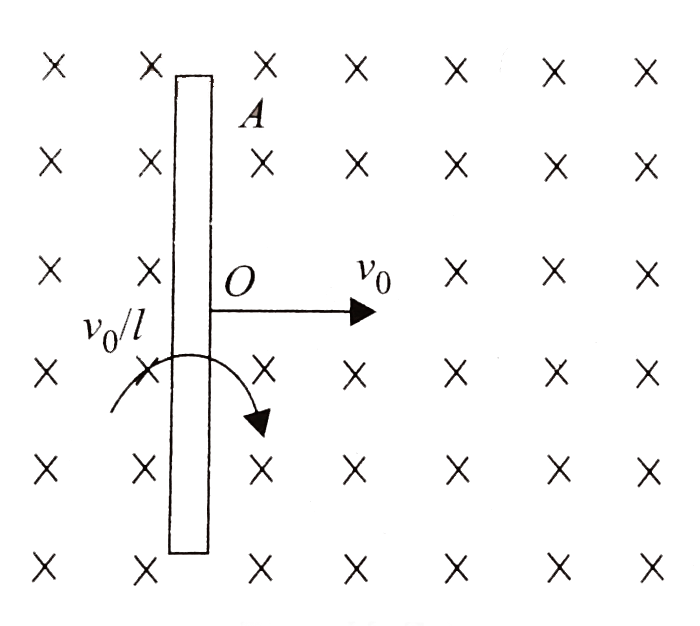 View Solution
View SolutionA mechanism consists of a part which is translated with a velocity u and a rod AB of length L and mass M hinged at A The rod rotates about axis A with angular velocity ω the kinetic energy of rod when it is vertical as shown is
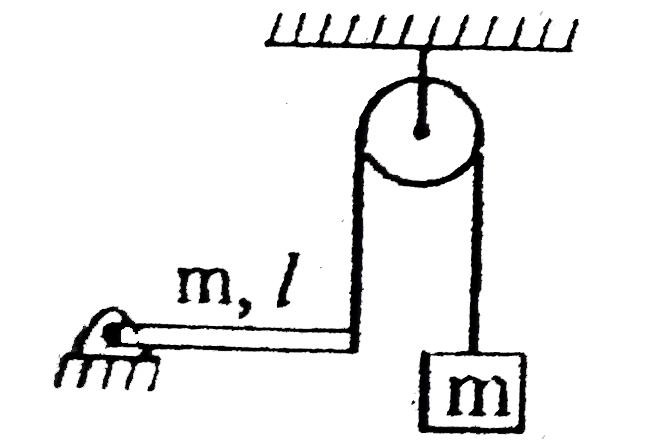 View Solution
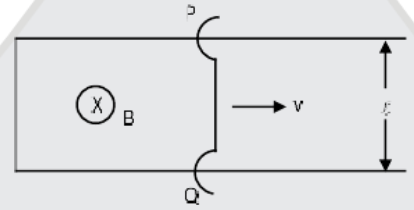
View SolutionA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
 View Solution
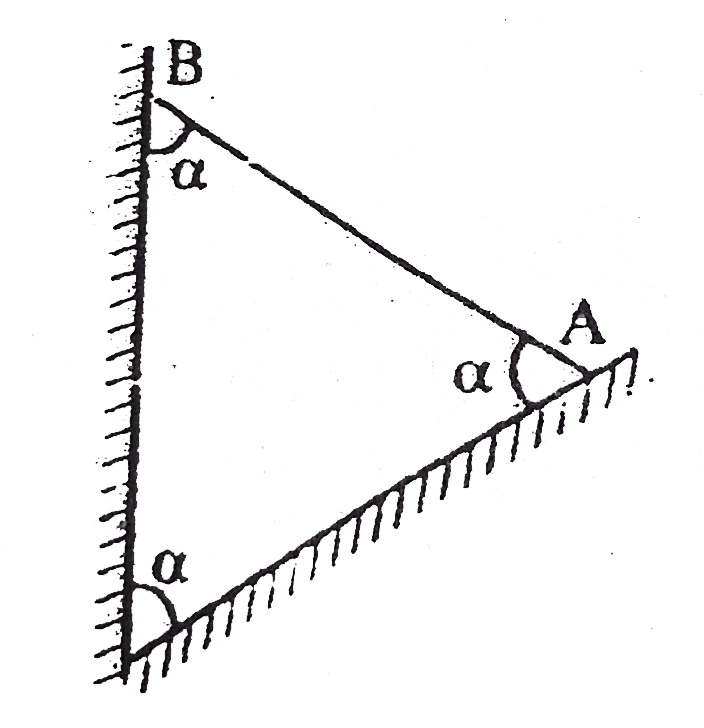
View SolutionIn the figure shown the end A of the rod of length L is being pushed down parallel to the inclined surface with a velocity =v let the velocity of end B=u and the angular velocity of the rod = ω then
 View Solution
View Solution

