The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by y=(0.4cm)sin[(0.314cm−1)x]cos[f(600πs−1)t].(a) What is the frequency of vibration ? (b) What are the positions of the nodes ? (c) What is the length of the string ? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration ?
Comparing with y=2asinkxcosωt we have
(1) ω=60π gives f=300Hz
(2) To get the position of nodes sinπx10=0
i.,e πx10=nπ where n=0,1,2....
Hence nodesoccur at x,0,10,20 cm.....
(3) since the string is in 3rd harmonic
l=3λ2 gives l=30cm
(4) Speed of wae v=fλ=300×20=60ms−1
Topper's Solved these Questions
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Theoretical questions :)
85 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Statement type questions:)
18 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)
10 Videos
Similar Questions
the equation for the vibration of a string fixed both ends vibration in its third harmonic is given by
y = 2 cm sin [(0.6cm−1x)×]cos[(500ps−1t]What is the position of node?
View SolutionThe equation for the vibration of a string fixed at both ends vibrating in its second harmonic is given by y=2sin(0.3cm−1)xcos((500πs−1)t)cm. The length of the string is :
View SolutionThe equation of a standing wave, produced on a string fixed at both ends, is y=(0.4cm)sin[(0.314cm−1)x]cos[(600πs−1)t] What could be the smallest length of the string ?
View SolutionA horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x,t)=(0.01m)sin[(62.8m−1x]cos[(628s−1)t]. Assuming p=3.14, the correct statement(s) is (are)
View SolutionThe vibrations of a string fixed at both ends are described by the equation y=(5.00mm)sin[(1.57cm−1)x]sin[(314s−1)t]
(a) What is the maximum displacement of particle at x = 5.66 cm ? (b) What are the wavelengths and the wave speeds of the two transvers waves that combine to give the above vibration ? (c ) What is the velocity of the particle at x = 5.66 cm at time t = 2.00s ? (d) If the length of the string is 10.0 cm, locate the nodes and teh antinodes. How many loops are formed in the vibration ?
View SolutionA thin taut string tied at both ends and oscillating in its third harmonic has its shape described by the equation y(x,t)=(5.60cm)sin[(0.0340radcm)x]sin[(50.0rads)t], where the origin is at the left end of the string, the x-axis is along the string and the y-axis is perpendicular to the string.
(a) Draw a sketch that shows the standing wave pattern.
(b)Find the amplitude of the two travelling waves that make up this standing wave.
(c) What is the length of the string?
(d) Find the wavelength, frequency, period and speed of the travelling wave.
(e) Find the maximum transverse speed of a point on the string.
(f) What would be the equation y(x,t) for this string if it were vibrating in its eighth harmonic?
View SolutionThe equation of a travelling wave on a string is y = (0.10 mm )sin[31.4m−1x+(314s−1)t]
View SolutionThe equation of a standing wave, set up in a string is, y=0.8 sin[(0.314cm−1)x]cos[(1200πs−1)t]. Calculate the smallest possible length of the living.
View SolutionA string fastened at both ends has successive resonances with wavelengths of 0.54 m for nth harmonic and 0.48 m for the (n+1) th harmonic and 0.48 m for the (n+1) th harmonic.
(a) Which harmonics are these?
(b) What is the length of the stirng?
(c) What is the wavelength of the fundamental frequency?
View SolutionFig. shows three different modes of vibration of a string of length I.
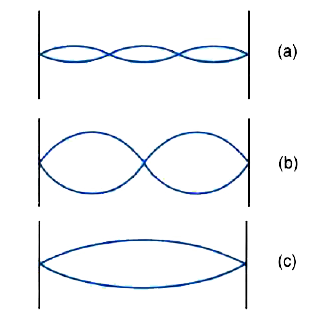
What is the ratio of wavelength between (b) and (a)?
View Solution
