The equation of a damped simple harmonic motion is md2xdt2+bdxdt+kx=0. Then the angular frequency of oscillation is
ω=(km−b24m2)1/2
ω=(km−b4m)1/2
ω=(km−b24m)1/2
ω=(km−b24m2)−1/2
The correct Answer is:A
(a)ω=√km−(b2m)2
Similar Questions
Knowledge Check
If a simple harmonic motion is represented by d2xdt2+αx=0, its time period is :
A2π√αB2παC2π√αD2παThe displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2π
The acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
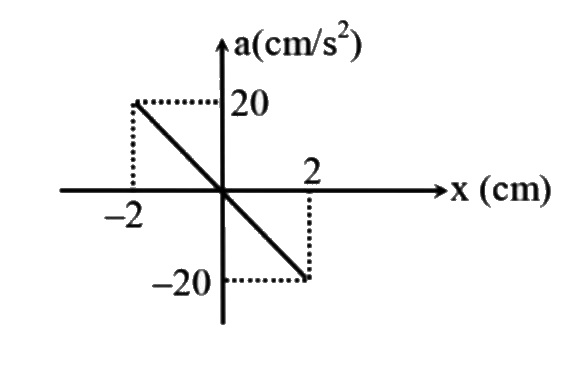
View SolutionThe acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionA particle executes simple harmonic motion according to equation 4d2xdt2+320x=0. Its time period of oscillation is :-
View SolutionIf a simple harmonic oscillator has got a displacement of 0.02m and acceleration equal to 2.0ms−2 at any time, the angular frequency of the oscillator is equal to
View SolutionThe position and velocity of a particle executing simple harmonic motion at t = 0 are given by 3 cm and 8cms−1 respectively . If the angular frequency of the particle is 2rad s−1 , then the amplitude of oscillation (in cm) is
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View Solution
