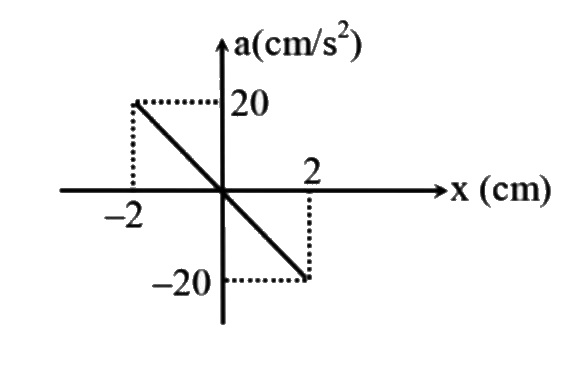
The acceleration-displacement $(a - X)$ graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

Video Solution

Text Solution

Verified by Experts

In SHM , $α = - ω^{2} x$
$β = - ω^{2} = (- α)$
$∴ β = ω^{2} = α$ (from graph)
and $ω = \sqrt{\frac{β}{α}}$
or $2 π f = \sqrt{\frac{β}{α}}$
or $f = \frac{1}{2 π} \sqrt{\frac{β}{α}}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3videos
MISCELLANEOUS KINEMATICS

Similar Questions

Knowledge Check

Question 1 - Select One
The differential equation of a particle executing simple harmonic motion along y-axis is
A $\frac{d^{2} y}{{d t}^{2}} + ω^{2} y = 0$
B $\frac{d^{2} y}{{d t}^{2}} + ω^{2} y^{2} = 0$
C $\frac{d^{2} y}{{d t}^{2}} - ω^{2} y = 0$
D $\frac{d y}{d t} + ω y = 0$

CENGAGE PHYSICS ENGLISH-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Exercise 4.1

Home
Ask Doubt
Profile